Régression parabolique non triviale

[lyceen95]

Pour tracer la courbe, comment fais-tu quand c'est une courbe plus simple ? Tu fais ça à la main (comme quand j'étais au lycée il y a 40 ans), ou tu utilises un logiciel dédié ?
Ici, avec un changement de repère, on se ramène à une équation v=a u². Donc un truc que tu sais à priori tracer.
Et c'est quoi le changement de repère en question ? c'est faire tourner la feuille d'un angle t.

[leon1789]

oui, bonne idée. Sans oublier une translation finale.

[sylvain231]

Ok j'utilise C++ avec OpenCV c'est pourquoi tracer cette courbe n'était pas si simple mais j'ai réussi. Cependant je n'ai pas réussi après deux jours de travail acharné à coder votre algo de calcul des paramètres de la parabole. Auriez-vous la gentillesse de me le donner en pseudo-code SVP ?
Sinon j'ai un second problème : maintenant je connais le sommet et deux points de chaque branche de la parabole, ma parabole est toujours translatée et tournée, comment trouver le theta et le a SVP ?
Merci beaucoup de votre aide en tout cas

[sylvain231]

Je précise un point pour chaque branche

[leon1789]

Je n'utilise pas le C++ pour faire des calculs mathématiques.
Si tracer une courbe n'est pas simple, alors je n'imagine pas comment vous allez faire pour déterminer les paramètres.

Pour votre second problème :
vous avez le sommet (X0 , Y0) et deux autres points (X1, Y1) et (X2, Y2) de la parabole, alors là, c'est simple, il suffit de résoudre (avec un algorithme de calculs numériques) ce système d'équations en les inconnues a et t :

0 = a * ( cos(t) * (X1-X0) + sin(t) * (Y1-Y0) ) ^2 + sin(t) * (X1-X0) - cos(t) * (Y1-Y0)
0 = a * ( cos(t) * (X2-X0) + sin(t) * (Y2-Y0) ) ^2 + sin(t) * (X2-X0) - cos(t) * (Y2-Y0)

Par exemple :
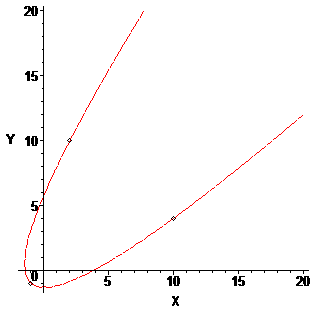
X0,Y0 := -1,-1 sommet
X1,Y1 := 2,10 point N°1
X2,Y2 := 10, 4 point N°2

Le système a pour solution : a = 0.43 et t = -0.71
la parabole est donnée par : 0 = 0.245*X^2 - 0.585*X - 0.422*X*Y - 1.40 - 0.816*Y + 0.182*Y^2

[leon1789]

On peut voir le problème sous forme géométrique. Une parabole, c'est l'ensemble des points équidistants d'un point F(le Foyer) et d'une droite D(la Directrice). Une parabole est donc définie par les coordonnées de ce Foyer (xF et yF) , et par l'équation de la droite (2 réels)

c'est une approche à creuser.

[sylvain231]

Donc si je comprends bien et c’était mon intuition première dans le second problème il n’y a qu’une solution et le fittage des points restants ne sert à rien

[sylvain231]

bonjour s'il y a qu'une solution et pas de fitting de points mon second problème ne me va plus. Pour mon premier problème auriez-vous une solution en pseudo-code SVP à me donner ?

[leon1789]

Bonjour,
je suis en train de réfléchir sur votre premier problème : l'ajustement.
Nous avons parlé de parabole y = a.x² , puis rotation d'angle t, et translation (c'est plutôt commode pour dessiner la courbe finale). Mais voilà, pourquoi la parabole y=ax² ? pourquoi pas x=ay² ? les calculs menés ensuite pour déterminer des valeurs satisfaisantes de t (pas si simple) puis de a (là, c'est facile) vont dépendre de plusieurs choix (ie. les fonctions à minimiser)

Je vais plutôt me pencher sur l'idée de Lycéen95 en passant par la détermination du foyer de la parabole : un point du plan, c'est 2 coordonnées, et notre problème est paramétré par 2 coefficients : c'est parfait !

PS.
Quand je pense que notre clown favori croit (il s'agit vraiment de croyance à son niveau, pas de maths) que la solution passe par une système à 6 équations à 6 inconnues, c'est vraiment n'importe quoi.

[Ben314]

Salut,
Sauf erreur, ça ne change rien de chercher la parabole sous la forme foyer-directrice vu que, si le foyer a pour coordonnées (a,b), alors l'équation de la directrice va être aX+bY+a^2+b^2=0 pour que le centre soit en (0,0) et dans la formule du calcul de la distance d'un point M:(X,Y) à la directrice il va y avoir une division par sqrt(a^2+b^2) ce qui incite plus que fortement à chercher les coordonnés du foyer sous forme polaire.
Et dans ce cas, ben on tombe exactement sur la formule déjà vue avec une rotation.

[leon1789]

chercher les coordonnés du foyer sous forme polaire.
Et dans ce cas, ben on tombe exactement sur la formule déjà vue avec une rotation.

ok

Je suis d'accord avec tes calculs :
en posant le foyer F de coordonnées (a,b) , le sommet étant toujours supposé (0,0) , alors l'équation de la droite directrice (D) est : a*(X+a) + b*(Y+b) = 0
La parabole cherchée est l'ensemble des points à équidistance de F et de (D) , autrement dit la parabole a pour équation :
(b*X - a*Y)^2 / (a^2+b^2) - 4*(a*X+b*Y) = 0

Disons que ça change que la nature des paramètres à déterminer : au lieu d'avoir a et t (avec cos(t) et sin(t) ), on a "uniquement" a et b sous forme fraction rationnelle. Peut-être plus sympathique.
Et aussi, ça indique peut-être une fonction "intrinsèque" à minimiser, à savoir la différence entre la distance de n points (Xi, Yi) au foyer et celle ces points à la droite directrice :
trouver a,b pour minimiser D1 ^2 + ... + Dn^2
en posant Di = ( b*Xi - a*Yi )^2 / (a^2+b^2) - 4*( a*Xi + b*Yi )

Mes arguments ne sont pas très solides, j'en conviens.

[Ben314]

Sinon, pour continuer l'idée de mon précédent fil, ce qu'il faut minimiser, c'est


Avec et

Donc tu commence par programmer le calcul des différents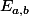 (après avoir retranché les coordonnées du centre) puis tu cherche le minimum de la fonction ci dessus par exemple en commençant par diviser [0,pi] en 1000 pour repérer où est le min, puis par dichotomie pour raffiner la valeur.

Et une fois ce min trouvé, tu calcule le coeff. de la parabole :

[leon1789]

tu calcules le coeff. de la parabole :

Ce a vaut cela car on est parti de la parabole Y=a * X^2. C'est arbitraire, on est d'accord ?

Si on avait pris pour référence la parabole X' = a' * Y' ^2 (même parabole, mais tournée), on aurait posé . Ok ?
et finalement ce a' n'aurait pas exactement la même valeur que le a au-dessus. Si ?
Ce qui, pour moi, est gênant. C'est pour cela que je penche du coté distance foyer droite.

[Ben314]

Le en question, c'est une fonction de et il correspond, au meilleur (au sens des moindres carré) coefficient pour la parabole si on fait une rotation de .
Donc si tu fait tourner la parabole, c'est bien toujours la même formule, mais pas avec le même .
Bref, ton c'est en fait un (même formule, mais pas la même valeur de ).

Et ce qu'on fait, c'est de prendre le meilleur (au sens des moindres carré) possible pour chaque et, pour ce là, de calculer la somme des carrés des écarts à la parabole : c'est de nouveau une fonction de et c'est elle qu'on cherche à minimiser.

[sylvain231]

OK merci et Eab c'est quoi exactement ?

[sylvain231]

et par dichotomie ça ne marche que pour des fonctions linéaires non ? mais là ce n'est pas linéaire

[sylvain231]

ah pardon Eab est défini, xi^a c'est bien puissance a ? et les (xi,yi) sont bien les points de mon nuage de points de départ ? mais dans ce cas a et b ne sont pas définis et on obtient une équation en theta mais comment trouver le a ?

[leon1789]

merci Ben, oui, je suis d'accord.
J'avais la même remarque en échangeant les X et Y (par symétrie par rapport à la première diagonale du plan), et je constate que le a ne change pas via les moindres carrés. OK !

[sylvain231]

Ah pardon a et b sont les paramètres de la fonction je n’ai pas les yeux en face des trous désolé

[leon1789]

Salut,
Sauf erreur, ça ne change rien de chercher la parabole sous la forme foyer-directrice vu que, si le foyer a pour coordonnées (a,b), alors l'équation de la directrice va être aX+bY+a^2+b^2=0 (...).

Je reviens avec un exemple simple, pour montrer que non, cela ne revient pas au même :
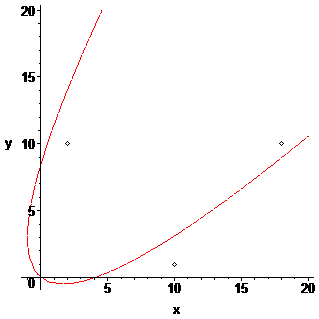
3 points (10;1) , (18;10) , (2;10)
le sommet est toujours en (0;0)

Le calcul issu du raisonnement rotation et coeff d'affinité donne ceci :
t := 0.665
a := 0.243
Et l'équation de la parabole obtenue :
0 = 0.144*x^2 - 0.226*x*y + 0.0887*y^2 - 0.592*x - 0.755*y

Graphe :