Régression parabolique non triviale

[sylvain231]

et voici la courbe de mon delta

[sylvain231]

ah je crois avoir compris ce qui se passe c'est le minimum en valeur absolue ou le plus grand négatif ?

[sylvain231]

ah c'est bon je crois avoir compris ce qui se passe ça marche sur un exemple, je vais tester sur un autre après mais avant je vous dis les modifs que j'ai faites : j'ai pris la valeur absolue de delta et j'ai mis le numérateur de a au carré, ce qui n'était pas le cas dans ton message

[sylvain231]

non ça ne marche pas ça n'a marché que sur un exemple

[sylvain231]

j'ai beau relire et relire mon code, j'ai bien codé exactement ce que tu avais mis, j'ai mis un bruit de 0 pour voir s'il me fittait une parabole mais non ça n'a rien à voir donc ton algo ne doit pas être bon ou alors j'ai sauté quelque chose

[Ben314]

Le delta(theta), c'est l'espérance d'un carré, donc, s'il n'y a pas d'erreur de programmation, il est systématiquement positif (donc ça sert à rien de prendre sa valeur absolue) : dans ton exemple, le delta minimum que je trouve, c'est 42.8 pour theta=139.5 degrés.
Et dans le cas du coefficient "a", il n'y a pas de carré au numérateur donc c'est bien a=-3.4e-5.

Bref, je trouve bien les même résultat que toi, mais par contre ton affichage graphique déconne.
Je pense que tu t'es gouré dans le sens de la rotation à appliquer au résultat : vu que dans le calcul on a tourné les points d'un angle theta, c'est que la courbe y=ax^2 du résultat, il faut la tourner d'un angle -theta et pas theta.

Et sinon, je pense que le résultat est correct (mais pas satisfaisant) : tu trouve une parabole de coeff. quasi nul, c'est à dire (dans le repère tourné) quasiment une droite horizontale et effectivement, dans ce repère là, les y-ax^2 sont petits vu que les y sont petits (vu le repère) et que les ax^2 sont petits (vu que a est quasiment nul).
Alors que si on regarde dans le tracé qu'a Léon, certes les points semblent proche de la parabole, mais les y-ax^2 doivent être quand même pas mal grand vu la façon dont on mesure l'écart (sur l'axe des y).

En bref, pour le type de données que tu as, la méthode que j'ai proposée ne convient pas vu qu'elle conclue que l'approximation par une droite (= parabole de coeficient nul) est meilleure que celle obtenue avec une "vraie" parabole. Donc :
1) Je pense que Léon n'a pas procédé comme je le préconisait (sinon il aurait trouvé comme toi que la meilleure approximation est quasiment une droite)
2) La façon de mesurer l'écart (sur l'axe des y) entre la parabole et le nuage de point ne convient pas pour ce type de données.

[sylvain231]

OK si tu tombe comme moi c'est que comme je le pensais (à part le problème d'affichage) le code est bon, as-tu une autre proposition STP ?

[Ben314]

Ben, déjà, comme "proposition", j'ai.... d'attendre que Léon explique comment lui il a fait vu qu'il a un résultat graphiquement bien plus satisfaisant . . .

Je réfléchi pour voir si j'ai autre chose à proposer.

[sylvain231]

ok merci beaucoup mais si ça se trouve Léon a utilisé un logiciel qui fitte automatiquement les paraboles, mais attendons sa réponse

[Ben314]

J'ai peut-être une idée : vu que de chercher 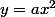conduit à trouver quasi nul comme meilleure approximation, on peut essayer à la place vu qu'en fait ça signifie que et donc va être bien plus grand lorsque proche de 0.

[sylvain231]

j'ai trouvé cet article est-il intéressant ?
https://www.sciencedirect.com/science/a ... 031830253X

[sylvain231]

a quasi nul dans cet exemple ! mais dans un autre je trouvais a = 7700 au lieu de 3

[Ben314]

Peut-être, sauf que, sans payer, tu as accès que à la partie "baratin" destinée à faire mousser l'article et pas au contenu.

[sylvain231]

ah non pardon c'était quand j'avais mis le numérateur au carré, non dans tous mes exemples (mais je n'en ai peut-être pas fait assez) a est presque nul

[Ben314]

et où et .

Le qui minimise est qui donne


avec ensuite

[sylvain231]

ok je teste merci

[Ben314]

Sur ton exemple, je trouve ça :
theta=49.860000 (en degré) ; b=-4.775292e-01 ; a=-2.094113 (=1/b)

(avec un delta_min = 29.21308)

[leon1789]

Salut,

Rebonjour,
de quel rigolo de service parlez-vous ?
Bonne journée

un gars qui donne des leçons, prétend qu'il sait résoudre des situations compliquées, alors qu'il ne sait pas faire les exos de bases. Ce qu'il adore, c'est surveiller et insulter les gens (sur un autre forum).
Par exemple, il suit notre discussion et il affirme que ton sujet est "complètement bidon et sans intérêt." Et je t'en passe des meilleurs.

[leon1789]

1) Je pense que Léon n'a pas procédé comme je le préconisait (sinon il aurait trouvé comme toi que la meilleure approximation est quasiment une droite)

si si, en commençant par translater, puis poser :

Xt := expand(cos(t)*X - sin(t)*Y)
Yt := expand(sin(t)*X + cos(t)*Y)

j'ai recherché numériquement le t minimisant la fonction que tu donnes, à savoir celle-ci :

add(Yt[i]^2, i=1..n) - (add(Xt[i]^2 * Yt[i], i=1..n)^2 / add(Xt[i]^4, i=1..n)) ;

puis calculé le a.

a := add(Xt[i]^2*Yt[i], i=1..n) / add(Xt[i]^4, i=1..n) ;

Attention au problème de signes dans les formules , surtout celle de l'équation de la parabole :

0 = a *( cos(t) * (x-S[1]) - sin(t) * (y-S[2]) ) ^2 - sin(t) * (x-S[1]) - cos(t) * (y-S[2])

Où S est le sommet fixé.

[sylvain231]

ah il me manque l'équation du b en fonction de c et de s STP !