Réductions des endomorphismes

[eratos]

salut!
Un truc bête pour commencer:
f un endomorphisme d'ev E, P, Q des polynômes,
pourquoi (P.Q)(f) = P(f) o Q(f)?

Ensuite: f endo E
Montrer que kerf=kerf² ssi kerf et imf sont supplémentaires.

f(f(x))=0. Que faire ici? kerf inter imf ={0} par hypothèse donc il s'ensuit que kerf c imf donc que dim kerf²=2 dim kerf...

je tourne en rond. :bad:

[Antho07]

Bonsoir,
On suppose que E = ker(f) + Im(f)
Prenons x dans ker(f²)
Donc x s'ecrit x= a +b avec a dans ker(f) et b dans Im( f)

but: f(x) = 0

Avec ça , plus en se rappelant ce que veut dire b est dans Im(f) , ça devrait rouler.

Cordialement.

[eratos]

merci =)
x= e+g ,e ds kerf et g ds imf
f(x)=f(e)+f(g)=f(g)=0 donc e+g est ds kerf...

Un autre:
on a dimE=n, f endomorphisme nilpotent de E
montrer: indice nilpotence de f=n ssi dim kerf=1
je ne vois pas comment m'y prendre :hum:

en fait dim ker=n, on peut chercher à prouver que dim ker =k 1<=k<=n

[eratos]

bonjour
je lutte pour comprendre ce qu'est un sous espace cyclique. :we:
on a le se cyclique de l'endomorphisme f engendré par x

on a que si dim, {} est une base de
Donc j'essaye de voir pourquoi on a ça, à partir de la définition de base mais je m'en sors pas, y aurait t'il un résultat utile pour le prouver plus facilement?

[eratos]

salut et bonne année à tous =)
voilà j'ai une matrice (A):
-------
0 2 -1|
3 -2 0|
-2 2 1|
--------

On me demande de la diagonaliser. Donc je trouve facilement les valeurs propres qui ne sont ni plus ni moins que les racines du polynome caractéristique de la matrice.
est scindé à racines simple donc on peut diagonaliser.
Autrement dit on a D une matrice diagonale tel que A=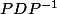 où P est une matrice de changement de base.

Comment je trouve D? Je l'ai fait en explicitant P puis P^{-1}, enfin en calculant D. Mais c'est extrêmement laborieux, du coup je cherche une méthode plus simple. A supposer qu'elle existe :help:

[eratos]

[eratos]

salut, comment faire une belle matrice 4 *4?

Voilà mon code, qu'est-ce qui va pas? :triste:
$ \begin{pmatrix} -1&0&0&2 \\ 0&-1&2&0 \\ 2&-2&3&-2 \\ -2 & 0 & 0 & 3 \end{matrix} $