Récurrence polynôme
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 03 Mai 2019, 14:23
par mehdi-128 » 03 Mai 2019, 14:23
Bonjour,
Je bloquer dans l'hérédité sur cette récurrence.
Soit

. La propriété
)
est :
" Si =n , x \mapsto P(x)e^{\lambda x}) admet une primitive sur
admet une primitive sur  de la forme
de la forme  e^{\lambda x}) où
où =n) "
"La propriété est vraie au rang

Une primitive de

est

avec
=0)
Je n'arrive pas à faire l'hérédité.
Supposons que pour un rang

fixé on ait :
=n+1)

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 03 Mai 2019, 18:07
par Sa Majesté » 03 Mai 2019, 18:07
Salut,
Pour une démonstration par récurrence, il faut trouver un moyen de relier la propriété au rang n+1 et la propriété au rang n.
On peut donc penser à une intégration par parties.
-
aviateur
 par aviateur » 03 Mai 2019, 18:55
par aviateur » 03 Mai 2019, 18:55
Bjr
Jamais je n'aurai fait une récurrence là dessus. Il faudrait peut être revoir ta rédac. pour n=0 qui laisse à désirer.
Et puis C=0 ça va pas.
Sinon tu peux améliorer l'exo en donnant le calcul explicite de Q.
Si on désigne par
})
l'opérateur de dérivation j fois alors tu peux démontrer que
^j}{\lambda ^{j+1}} D^{(j)}) P)
est la solution
Modifié en dernier par aviateur le 03 Mai 2019, 22:16, modifié 1 fois.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 03 Mai 2019, 20:33
par mehdi-128 » 03 Mai 2019, 20:33
Mon livre demande de faire par récurrence, sûrement parce que la chapitre sur les polynôme n'a pas encore été abordé.
J'ai réussi :
Une primitive sur

de la fonction
e^{\lambda x})
est :
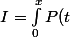e^{\lambda t} dt)
Les fonctions :
)
et

sont de classe

sur

.
Donc
e^{\lambda x}}{\lambda}- \dfrac{P(0)}{\lambda} + \dfrac{1}{\lambda} \int_0^x P'(t)e^{\lambda t} dt)
D'après l'hypothèse de récurrence, une primitive de
e^{\lambda t})
est
e^{\lambda t})
car
=n)
Avec
=n)
Alors :
e^{\lambda x}}{\lambda}- \dfrac{P(0)}{\lambda} + \dfrac{1}{\lambda} (R(x) e^{\lambda x} -R(0)))

admet une primitive sous la forme :
- \dfrac{1}{\lambda}(P(0)+R(0)))
Avec
= \dfrac{1}{\lambda} (P(x) - R(x)))
avec
=\max(\deg(P),\deg(R))=n+1)
- \dfrac{1}{\lambda}(P(0)+R(0)))
est une primitive de

donc
))
est aussi une primitive de

car la dérivée d'une constante est nulle.
D'où le résultat.
-
aviateur
 par aviateur » 03 Mai 2019, 22:34
par aviateur » 03 Mai 2019, 22:34
mehdi-128 a écrit: Mon livre demande de faire par récurrence, sûrement parce que la chapitre sur les polynôme n'a pas encore été abordé.
Je vois pas le rapport. Et puis un exercice sur les polynômes ça veut dire qu'on sait ce qu'est un polynôme.
mehdi-128 a écrit:J'ai réussi : ???
Sous ton pseudo @Ram... il n'y a personne qui t'a donné la solution?
Et puis tout de même, c'est un peu con de faire une récurrence pour une démo en 2,3 lignes. Il y aurait un tordu qui impose une récurrence?
L'application linéaire de 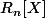 dans
dans 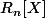 définie par
définie par =Q'+\lambda Q) est évidemment injective donc bijective. En particulier si P est de degré n, l'unique antécédent
est évidemment injective donc bijective. En particulier si P est de degré n, l'unique antécédent  de P par f est degré n exactement et répond à la question.
de P par f est degré n exactement et répond à la question.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Mai 2019, 15:07
par mehdi-128 » 05 Mai 2019, 15:07
Votre méthode ne peut pas être utilisée à ce stade étant donné que les applications linéaires et espaces vectoriels sont abordés bien après dans le livre.
Puis on est dans le paragraphe "intégration par parties" donc...
Je n'ai pas compris d'où sort le :
=Q'+ \lambda Q)
. Je ne comprends pas votre solution. C'est où que vous parlez de primitive ?
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 05 Mai 2019, 16:45
par tournesol » 05 Mai 2019, 16:45
Cherchons une fonction Q telle que
e^{\lambda x})
soit une primitive de
e^{\lambda x})
, P étant une fonction continue quelconque .
e^{\lambda x})
est une primitive de
e^{\lambda x})
ssi
e^{\lambda x})'=P(x)e^{\lambda x})
ssi
e^{\lambda x}+Q(x)\lambda e^{\lambda x}=P(x)e^{\lambda x})
ssi
+\lambda Q(x))e^{\lambda x}=P(x)e^{\lambda x})
ssi (car

n'est jamais nul)
+\lambda Q(x)=P(x))
Soit f l'application de
)
dans
)
définie par
=Q'+\lambda Q)
On a donc :
e^{\lambda x})
est une primitive de
e^{\lambda x})
ssi
Q est un antécédent de P par F .
Dans le cas de la restriction de f aux polynômes de degrés n , on a effectivement le traitement ALGEBRIQUE concis et élégant proposé par aviateur .
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Mai 2019, 19:02
par mehdi-128 » 05 Mai 2019, 19:02
merci Tournesol.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités