Salut, dans une correction d'épreuves il est écrit que, puisque la matrice M a un rayon spectral strictement inférieur à 1, M^n tends vers la matrice nulle en l'infini
Je trouve ce résultat très douteux ...Pourriez-vous m'aiguiller?
Merci
Rayon spectral strictement inférieur à 1
14 messages
- Page 1 sur 1
Salut,
Oui c'est vrai, et ce sont même des conditions équivalentes.
=> (1ère implication)
Supposons que M^n tend vers 0 (matrice nulle) en l'infini, puisque pour tout u de C^n on a ||M^n u|| <= |||M^n||| ||u|| (avec ||.|| norme matricielle sur C^n et |||.||| sa norme matricielle subordonnée), on a: (M^n u) qui tend vers 0 en l'infini.
Supposons de plus p(M)>=1 (rayon spectral), alors soit v une valeur propre de M telle que p(M)=|v|>=1 et soit x un vecteur propre associé à v (x différent de 0), alors Mx=vx puis M²x=v²x ...
M^n x = v^n x
donc: ||M^n x||=|v|^n ||x|| >= ||x||>0
donc: M^n x ne tend pas vers 0 en l'infini
on obtient donc une contradiction et p(M)<1
<= (2ème implication)
Si p(M)<1 et soit eps>0 tel que p(M)+eps<1, alors il existe une norme matricielle subordonnée telle que ||M||<=p(M)+eps<1 et ||M^n||<=||M||^n qui tend vers 0 en l'infini si ||M||<1, d'où le 1er résultat.
Oui c'est vrai, et ce sont même des conditions équivalentes.
=> (1ère implication)
Supposons que M^n tend vers 0 (matrice nulle) en l'infini, puisque pour tout u de C^n on a ||M^n u|| <= |||M^n||| ||u|| (avec ||.|| norme matricielle sur C^n et |||.||| sa norme matricielle subordonnée), on a: (M^n u) qui tend vers 0 en l'infini.
Supposons de plus p(M)>=1 (rayon spectral), alors soit v une valeur propre de M telle que p(M)=|v|>=1 et soit x un vecteur propre associé à v (x différent de 0), alors Mx=vx puis M²x=v²x ...
M^n x = v^n x
donc: ||M^n x||=|v|^n ||x|| >= ||x||>0
donc: M^n x ne tend pas vers 0 en l'infini
on obtient donc une contradiction et p(M)<1
<= (2ème implication)
Si p(M)<1 et soit eps>0 tel que p(M)+eps<1, alors il existe une norme matricielle subordonnée telle que ||M||<=p(M)+eps<1 et ||M^n||<=||M||^n qui tend vers 0 en l'infini si ||M||<1, d'où le 1er résultat.
Bonjour
A prouver! et c'est le point crucial de l'affaire.
Une methode est de trigonaliser dans
dans  , soit :
, soit : 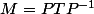 avec
avec  triangulaire supérieure et
triangulaire supérieure et  inversible, et d'utiliser une matrice diagonale variable
inversible, et d'utiliser une matrice diagonale variable 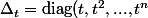) (
( réel variable non nul ) en remarquant que la matrice
réel variable non nul ) en remarquant que la matrice ^{-1} T D_t) tends vers une matrice diagonale lorsque
tends vers une matrice diagonale lorsque  tends vers
tends vers 
MacManus a écrit:alors il existe une norme matricielle subordonnée telle que ||M||<=p(M)+eps
A prouver! et c'est le point crucial de l'affaire.
Une methode est de trigonaliser
MacManus a écrit:Je suis bien d'accord
Merci MacManus pour la confirmation , et j'ajoute à l'interessé qu'il aura besoin de prouver que si
newman a écrit:Salut, dans une correction d'épreuves il est écrit que, puisque la matrice M a un rayon spectral strictement inférieur à 1, M^n tends vers la matrice nulle en l'infini
Je trouve ce résultat très douteux ...Pourriez-vous m'aiguiller?
Merci
en fait rayon <1 equivaut a l'existence d 'une norme matricielle telle que ||M|| < 1
et donc ||M^n|| <= ||M||^n qui tend vers 0
ismath
newman a écrit:Je trouvais ce résultat douteux car il me semble assez puissant...
Salu newman:
Si tu n'arrives pas à rédiger la preuve compléte préviens moi.
J'avais l'intention de mettre (sur ma pge pers) un petit article qui rassembe : rayon spectral, quotient de Rayleigh, normes subordonnées , qui est un incontournables pour les spés ...
Je crois que c'est le bon moment de le rédiger.
newman a écrit:en fait c'est bon j'ai trouvé...
Salut
Tant mieux.
Si tu veux consulter l'épreuve de centrale 2005 la prmière partie traite complétement ce sujet.
Pour ma page , je suis entrain de reconstruire une nouvelle version et tu peux déjà la visite www.marocprepa.com .
Je metterai le sujet dans la rubrique 'News' sous rubriques : 'articles de mathématiques'.
PS: Si tu ne trouves pas l'épreuve de centrale (il y'a un corrigé aussi), tu peux chercher dans le site de l'UPS : c'est ici (il suffit de selection l'année 2005 et l'école centrale (section MP)).
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
