Je sais que pour trouver R, il faut que j'utilise la formule
Rayon de convergence
6 messages
- Page 1 sur 1
Rayon de convergence
Bonjour :we: , je traite un exercice dans lequel je dois determiner le rayon de convergence de séries entières  . Le cas pour lequel je n'y arrive pas est le suivant:
. Le cas pour lequel je n'y arrive pas est le suivant:
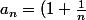^n - e)
Je sais que pour trouver R, il faut que j'utilise la formule et que
et que  est la limite que je trouve soit en utilisant le méthode de d'Alembert (
est la limite que je trouve soit en utilisant le méthode de d'Alembert (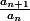 ) soit Cauchy (
) soit Cauchy (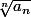 ). Donc si quelqu'un peut me mettre sur la piste, merci d'avance! :we: :happy2:
). Donc si quelqu'un peut me mettre sur la piste, merci d'avance! :we: :happy2:
Je sais que pour trouver R, il faut que j'utilise la formule
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
