Démontrer que x=(7+5;)2)^1/3 +(7-5;)2)^1/3
Est un nombre rationnel
Rationnel
8 messages
- Page 1 sur 1
Polytechnique enp a écrit:Démontrer que x=(7+5;)2)^1/3 +(7-5;)2)^1/3
Est un nombre rationnel
Voici la première solution pas du tout élégante à laquelle je pense :
En élevant tout à la puissance 3 :
x³ = (7+5;)2) + (7-5;)2) + 3(7+5;)2)^(2/3)*(7-5;)2)^(1/3) + 3(7+5;)2)^(1/3)*(7-5;)2)^(2/3)
= 14 + 3(7+5;)2)^(2/3)*(7-5;)2)^(1/3) + 3(7+5;)2)^(1/3)*(7-5;)2)^(2/3)
= 14 + 3*[(7+5;)2)^(2/3)*(7-5;)2)^(1/3) + (7+5;)2)^(1/3)*(7-5;)2)^(2/3)]
= 14 + 3*((7+5;)2)(7-5;)2))^(1/3)*[(7+5;)2)^(1/3) + (7-5;)2)^(1/3)]
= 14 - 3*[(7+5;)2)^(1/3) + (7-5;)2)^(1/3)]
Donc x³ + 3x - 14 = 0
Procédons désormais par analyse-synthèse. Supposons qu'il n'existe qu'une et une seule solution rationnelle, s'écrivant p/q (q non nul), à cette équation (c'est ce qu'on cherche).
Alors cette solution satisfait p³/q³ + 3p/q - 14 = 0, i.e. p³/q³ + 3pq²/q³ - 14q³/q³ = 0 ou encore
p³ + 3pq² - 14q³ = 0
i.e. q(14q² - 3pq) = p³
ce qui veut dire que q divise p³. Or p et q sont premiers entre eux donc q divise 1. Mieux encore, q = 1.
De même, on a p(p² + 3q²) = 14q³
Donc p divise 14. A partir de là, nous n'avons pas 36000 choix. Soit p = 2, soit p = 7. Or x = 7 ne satisfait pas à l'équation x³ + 3x - 14 = 0, donc x = 2.
Inversement, 2 satisfait bien à x³ + 3x - 14 = 0.
Mais... je sais pas si c'est propre
Je trouve sauf avis contraire de ceux qui sont plus initié que moi que votre solution est bien structurée. Pour ma part jai procédé comme suit :
On a x =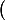 7 + 5
7 + 5
^{\frac{1}{3}})
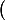 7 - 5
7 - 5
^{\frac{1}{3}})
donc = 7 + 5
= 7 + 5 + 7 - 5
+ 7 - 5 + 3
+ 3 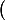
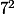 (5
(5
^2)
^{\frac{1}{3}})
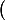 (7 + 5
(7 + 5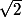
^{\frac{1}{3}}) + (7 - 5
+ (7 - 5
^{\frac{1}{3})
) .
.
= 14 + 3 (49 - 50) x
= 14 3 x ,
donc on a : + 3 x 14 = 0 qui a pour racine triviale 2,
+ 3 x 14 = 0 qui a pour racine triviale 2,
donc + 3 x 14 = (x 2)(
+ 3 x 14 = (x 2)( + 2 x + 7),
+ 2 x + 7),
donc lensemble des racines de ( + 3 x 14 = 0) est : {2, -1 - i
+ 3 x 14 = 0) est : {2, -1 - i 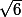 , -1 + i
, -1 + i 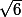 } ,
} ,
donc la seule racine rationnel (et plus N) est 2.
N) est 2.
On a x =
donc
= 14 + 3 (49 - 50) x
= 14 3 x ,
donc on a :
donc
donc lensemble des racines de (
donc la seule racine rationnel (et plus
aymanemaysae a écrit:Je trouve sauf avis contraire de ceux qui sont plus initié que moi que votre solution est bien structurée. Pour ma part jai procédé comme suit :
On a x =7 + 5
^{\frac{1}{3}})
7 - 5
donc= 7 + 5
+ 7 - 5
+ 3
(5
^{\frac{1}{3}})
(7 + 5
+ (7 - 5
.
= 14 + 3 (49 - 50) x
= 14 3 x ,
donc on a :+ 3 x 14 = 0 qui a pour racine triviale 2,
donc+ 3 x 14 = (x 2)(
+ 2 x + 7),
donc lensemble des racines de (+ 3 x 14 = 0) est : {2, -1 -
, -1 +
} ,
donc la seule racine rationnel (et plus \in N) est 2.
Tu es sûr ? Je doute que X² + 2X + 7 admette des racines réelles.
Salut,
C'est la méthode de Cardan et pour retrouver l'équation, il suffit de suivre la méthode "à l'envers" :
Si ,
,  et
et  alors
alors  et
et  .
.
Donc+(U+V)\big(3UV+3\big)=(U+V)^3+3(U+V)-14=x^3+3x-14)
EDIT : en fait, il y a plus simple vu que et que
et que  ...
...
C'est la méthode de Cardan et pour retrouver l'équation, il suffit de suivre la méthode "à l'envers" :
Si
Donc
EDIT : en fait, il y a plus simple vu que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
