Bonjour,
J'éprouve des difficultés à déterminer le rang de la matrice carrée d'ordre n définie par a_{ij}=1 si |i-j|<=1 et 0 sinon. je n'ai pas encore vu la notion de déterminant et je ne parviens à mettre la matrice sous forme échelonnée.
Merci pour votre aide
Rang d'une matrice
8 messages
- Page 1 sur 1
Re: rang d'une matrice
Tu fais comme si ta matrice A est celle d'un endomorphisme u et tu calcules ker(u)
Re: rang d'une matrice
Oui mais il faut résoudre le système :
a1+a2=0
a(k-1)+a(k)+a(k+1)=0 pour k=2...n-1
a(n-2)+a(n)=0
ce qui est loin d'être évident.
a1+a2=0
a(k-1)+a(k)+a(k+1)=0 pour k=2...n-1
a(n-2)+a(n)=0
ce qui est loin d'être évident.
Re: rang d'une matrice
Bonjour
Une remarque tout de même, le déterminant ne donne pas toujours le rang. S'il est non nul le rang est maximum. Mais est-ce le cas ici?
D'autre part échelonner la matrice pourquoi pas mais le travail risque de dépendre de n.
Alors je pense que le mieux est de déterminer le noyau de la matrice Ker(M) qui donne le rang grâce au théorème du rang.
Soit donc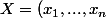^t) un vecteur du noyau, i.e MX=0.
un vecteur du noyau, i.e MX=0.
Ce qui est équivalent au système suivant

où j'ai ajouté et
et  pour uniformiser les équations. (on pose donc
pour uniformiser les équations. (on pose donc  ).
).
Les forment donc une suite récurrente dont chaque terme dépend linéairement des deux précédents. La suite
forment donc une suite récurrente dont chaque terme dépend linéairement des deux précédents. La suite ) est donc de la forme
est donc de la forme 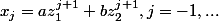
où et
et 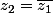 sont les racines de
sont les racines de 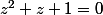 .
.
Mais donc b=-a. On a alors
donc b=-a. On a alors 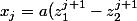)
Mais on a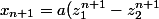=0)
Or pour
pour 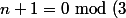) alors dim Ker(f)=1 et le rang est n-1.
alors dim Ker(f)=1 et le rang est n-1.
Si alors a=0 et X=0, i;e M est inversible est le rang est maximal = n.
alors a=0 et X=0, i;e M est inversible est le rang est maximal = n.
En résumé il y a 2 rangs possibles n-1 pour n=2,5,8,... et n sinon.
Une remarque tout de même, le déterminant ne donne pas toujours le rang. S'il est non nul le rang est maximum. Mais est-ce le cas ici?
D'autre part échelonner la matrice pourquoi pas mais le travail risque de dépendre de n.
Alors je pense que le mieux est de déterminer le noyau de la matrice Ker(M) qui donne le rang grâce au théorème du rang.
Soit donc
Ce qui est équivalent au système suivant
où j'ai ajouté
Les
où
Mais
Mais on a
Or
Si
En résumé il y a 2 rangs possibles n-1 pour n=2,5,8,... et n sinon.
Modifié en dernier par aviateur le 10 Avr 2019, 13:11, modifié 4 fois.
Re: rang d'une matrice
Génial
Merci infiniment aviateur !
Je n'aurais jamais penser à utiliser une suite récurrente linéaire d'ordre 2.
Ca plane pour toi si j'ose dire !
Merci infiniment aviateur !
Je n'aurais jamais penser à utiliser une suite récurrente linéaire d'ordre 2.
Ca plane pour toi si j'ose dire !
Re: rang d'une matrice
Merci, je suis aviateur et quand je coupe le moteur je plane.
Modifié en dernier par aviateur le 10 Avr 2019, 13:09, modifié 4 fois.
Re: rang d'une matrice
On peut aussi essayer de procéder par récurrence:
on écrit les 4 dernières équations




on a rapidement et les valeurs de
et les valeurs de  jusqu'à
jusqu'à  dépendent du cas n-3 .
dépendent du cas n-3 .
On a ensuite et
et 
Donc si N est la matrice d'une base de ker(u) dans le cas n-3 , j'obtiens la matrice d'une base de ker (u) dans le cas n en lui rajoutant une ligne nulle (x_2=0) , suivie de l'opposée de la ligne n-3 puis de la ligne n-3 .
Donc le rang dans le cas n est egal au rang dans le cas n-3
on écrit les 4 dernières équations
on a rapidement
On a ensuite
Donc si N est la matrice d'une base de ker(u) dans le cas n-3 , j'obtiens la matrice d'une base de ker (u) dans le cas n en lui rajoutant une ligne nulle (x_2=0) , suivie de l'opposée de la ligne n-3 puis de la ligne n-3 .
Donc le rang dans le cas n est egal au rang dans le cas n-3
Re: rang d'une matrice
ERREUR
C'est la dimension de ker u qui est la même dans le cas n et dans le cas n-3 .
Il en résulte que = rang(A_{n-3}) +3)
C'est la dimension de ker u qui est la même dans le cas n et dans le cas n-3 .
Il en résulte que
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
