Racines complexes d'un polynome
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
BonbonB
- Membre Naturel
- Messages: 14
- Enregistré le: 29 Déc 2013, 20:54
-
 par BonbonB » 29 Déc 2013, 21:05
par BonbonB » 29 Déc 2013, 21:05
Bonjour,
dans mon exercice, on considère le polynôme: P(x)=10x^10-x^9-x^8... -x-1.
j'ai fait la première question, soit de montrer que:
P(x)=(x-1)(10x^9+9x^8+8x^7+...2x+1)
Par la suite, il faut montrer que les
racines complexes de P(x) sont de
module inférieur OU égal à 1, puis que le polynôme admet qu'une
unique racine de module 1.
C'est ici que je bloque depuis un bon moment.
Merci


-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 30 Déc 2013, 15:07
par Ben314 » 30 Déc 2013, 15:07
Salut,
Si z est un complexe tel que
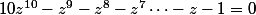
alors

En faisant passer tout les termes à gauche et en factorisant

(comme dans la question 1), tu en déduit que

.
De plus, il ne peut y avoir égalité que si les complexes

sont colinéaires à coeff. positifs ce qui donne
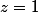
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
BonbonB
- Membre Naturel
- Messages: 14
- Enregistré le: 29 Déc 2013, 20:54
-
 par BonbonB » 30 Déc 2013, 20:51
par BonbonB » 30 Déc 2013, 20:51
Donc en fait on obtient:
10z^10-z^9-z^8-z^7...-z-1 =
(z-1)(10z^9+9X^8+...2X+1) =
z-1=<0
en mettant module partout.
c'est ça?
Je ne comprends pas quand vous dites que les complexes sont colinéaires à coefficients positifs...
-
Tiruxa
- Membre Relatif
- Messages: 460
- Enregistré le: 22 Oct 2013, 09:21
-
 par Tiruxa » 31 Déc 2013, 08:27
par Tiruxa » 31 Déc 2013, 08:27
BonbonB a écrit:Je ne comprends pas quand vous dites que les complexes sont colinéaires à coefficients positifs...
Cela signifie qu'ils ont même argument
Démonstration dans le cas de 2 complexes (facilement généralisable) ici :
http://www.ilemaths.net/forum-sujet-537369.htmlDans ce cas (module de z égal à 1) 1 et z ont donc même argument cela signifie que z est réel positif.
Le seul réel positif de module 1 est bien sûr 1.
Donc la seule racine de module 1 est 1.
-
BonbonB
- Membre Naturel
- Messages: 14
- Enregistré le: 29 Déc 2013, 20:54
-
 par BonbonB » 31 Déc 2013, 21:06
par BonbonB » 31 Déc 2013, 21:06
L'égalité : 10z^10-z^9-z^8-z^7...-z-1 = 0 est possible si z^9, z^8...,z,1 ont même argument?
je ne comprends pas :triste:
-
Tiruxa
- Membre Relatif
- Messages: 460
- Enregistré le: 22 Oct 2013, 09:21
-
 par Tiruxa » 01 Jan 2014, 17:09
par Tiruxa » 01 Jan 2014, 17:09
BonbonB a écrit:L'égalité : 10z^10-z^9-z^8-z^7...-z-1 = 0 est possible si z^9, z^8...,z,1 ont même argument?
je ne comprends pas :triste:
Non, si on a l'égalité

alors 1, z, z² etc ont même argument
-
BonbonB
- Membre Naturel
- Messages: 14
- Enregistré le: 29 Déc 2013, 20:54
-
 par BonbonB » 01 Jan 2014, 17:39
par BonbonB » 01 Jan 2014, 17:39
Ah d'accord :we: et comment on démontre que:
|z^9+z^8+z^7...+z+1| inférieur ou égal |z^9|+|z^8|+|z^7|...+|z|+|1|?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 02 Jan 2014, 14:06
par Ben314 » 02 Jan 2014, 14:06
En utilisant 8 fois le résultat archi connu qui dit que

(le plus court chemin est le ligne droite)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
