Bonjour,
raito123 a écrit:1/Si dans un anneau

on a
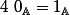
alors je pense que

serai un corps !! est-ce juste?
Non. Si
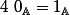
, alors l'anneau est l'anneau nul ({0}), et l'anneau nul n'est pas un corps.
Un corps, ça a minimum 2 éléments, à savoir 0 et 1. (Et j'arrête tout de suite les théoriciens qui voudraient parler du corps à un élément. Pitié, pas ici...)
2/D'aprés ce que j'ai compris du cours que j'ai trouver sur le net une K-algébre est un anneau A qui est en même temps un espace véctoriel : c'est bon !?
Oui, plus un axiome de compatibilité : (a·x)×(b·y) = (ab)·(x×y) pour a et b dans ton corps et x et y dans ton algèbre.
Sinon comment montrer "un sous-K-algébre"? en montrant que c'est un sous-anneau et un sous-espace véctoriel??
Pour montrer que E' est une sous-algèbre de E, il faut et suffit de montrer que c'est un sous-espace vectoriel de E, contenant 1, et stable par produit.
On m'a demander de montrer un sous-K-algébre de IR : ça veut dire que les coefficients de A sont dans IR !??
Mmmh ? Précise ta question.

est naturellement muni d'une structure de

-algèbre, mais pas de K-algèbre pour K quelconque...
3/ le signe K[X] veut dire l'ensemble de polinome de coefficients dans K ?
Oui. Sauf que c'est "polynôme".
4/ pour montrer que deux ensemble sont homomorphe doit-on trouver un homomorphisme ou y a une methode plus simple ?
Ben oui, c'est la méthode de base. Enfin si tu précises rien de plus c'est clair qu'on voit guère quoi faire d'autre...
5/ dans un exo que je fais en ce moment même on me demande de montrer que
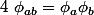
(indicateur d'euler) avec pgcd(a,b) = 1 tout en sachant que

et

sont isomorphe !! donc phi doit être un isomorphisme de Z/abZ vers Z/aZ*Z/BZ muni de la lois multiplier mais comment faire !!?
L'indicatrice d'Euler ne peut pas être un isomorphisme de Z/abZ vers Z/aZ*Z/bZ parce que ça n'a pas de sens. En effet, l'indicatrice d'Euler est à valeurs dans les nombres entiers...
En revanche, tu peux dire qu'il y a exactement
)
générateurs du groupe Z/abZ (ce sont tous les nombres premiers avec ab). Comme un couple (x,y) est générateur de Z/aZ*Z/bZ si et seulement si x est générateur de Z/aZ et y générateur de Z/bZ, tu peux en déduire le nombre de générateurs de Z/aZ*Z/bZ. Comme les deux groupes sont isomorphes, c'est fini.
