QCM Ensam
22 messages
- Page 1 sur 2 - 1, 2
Re: QCM Ensam
Bonjour,
Peut être qu'il manque quelque chose dans cet énoncé, non ?
Que faut il faire au juste, trouver le ou les couples (a;b) tels que N soit premier ?
Peut être qu'il manque quelque chose dans cet énoncé, non ?
Que faut il faire au juste, trouver le ou les couples (a;b) tels que N soit premier ?
Re: QCM Ensam
salut
première idée :
si a est pair ... surement pas ...
que se passe-t-il si a est impair ?
deuxième idée :^2 - ... ?)
première idée :
si a est pair ... surement pas ...
que se passe-t-il si a est impair ?
deuxième idée :
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: QCM Ensam
Non l énoncé est exactement celui que j ai ecrit car il s agit d un QCM pas de redaction mais je dois juste coché... j ai deja essayé la tecnique que vous m avais suggérer (a^4 + 4b ^ 4) = (a^2 +2b ^2) ^2 _ 4 ab caree
Mais je suis arrive a r1
Mais je suis arrive a r1
Re: QCM Ensam
un peu de sérieux ...
si tu veux de l'aide fais un effort de rédaction !!!
peux-tu répondre correctement à ma deuxième idée ?
si tu veux de l'aide fais un effort de rédaction !!!
peux-tu répondre correctement à ma deuxième idée ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: QCM Ensam
Non mais sérieusement je suis serieuse je l ai essayé avant en utilisant les regle d'arithmétique et tt et sa n a pas marcher sinnon je vien de m inscrire et je me demande comment vous arriver a rediger avec les symboles dnc je me contente decrire comme comme sa se que j aprenne a les utiliser....
Re: QCM Ensam
j ai deja essayé la tecnique que vous m avais suggérer (a^4 + 4b ^ 4) = (a^2 +2b ^2) ^2 _ 4 ab caree
Mais je suis arrive a r1
1/ je vois a^4, a^2 .... puis 2_4ab caree ....

2/ a r1 ...

3/ et dans le supérieur ... ne pas compléter cette égalité correctement ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: QCM Ensam
Non mais elle est correcte, cest juste que vous l avais lu de votre facons ^ sa c est a la puissance donc je jetais une autre fois un coup d'oeil ( a ^2. + 2 b^2) ^2 - 4(ab)^2
Re: QCM Ensam
Les QCM sont des choses que je ne connais pas vraiment mais si l’énoncé est celui que tu donnes au mot près alors la bonne case à cocher est "ça dépend".
Par exemple je connais un couple) tel que
tel que  est premier, et j'en connais toute une tripotée générant des entiers
est premier, et j'en connais toute une tripotée générant des entiers  composés (cf. la factorisation suggérée).
composés (cf. la factorisation suggérée).
Par exemple je connais un couple
Re: QCM Ensam
Bonsoir,
Si la question a été posée telle quelle, alors elle a été abominablement rédigée.
1- D'abord, si et
et  sont supposés réels, alors
sont supposés réels, alors  n'est a priori pas un entier, donc parler de nombre premier n'est pas très judicieux.
n'est a priori pas un entier, donc parler de nombre premier n'est pas très judicieux.
2- Ensuite, si l'on considère que et
et  sont des entiers, les exemples
sont des entiers, les exemples =(0,0)) et
et =(1,1)) montrent que la réponse est "ça dépend".
montrent que la réponse est "ça dépend".
3- Au fait, vu que c'est un QCM, quelles sont les réponses au choix ?
4- En fin de compte, la réponse proposée par zygomatique est la plus mathématiquement correcte (et se ramène d'ailleurs à une réponse du type "ça dépend").
Si la question a été posée telle quelle, alors elle a été abominablement rédigée.
1- D'abord, si
2- Ensuite, si l'on considère que
3- Au fait, vu que c'est un QCM, quelles sont les réponses au choix ?
4- En fin de compte, la réponse proposée par zygomatique est la plus mathématiquement correcte (et se ramène d'ailleurs à une réponse du type "ça dépend").
Re: QCM Ensam
Normalement ya 4 choix parmis eu ses deux choix premier ou pas un seul choix est correcte et vu le nombre a^4 + 4b^4 ne peut etre que premier ou pas ...
Re: QCM Ensam
Normalement ya 4 choix parmis eu ses deux choix premier ou pas un seul choix est correcte et vu le nombre a^4 + 4b^4 ne peut etre que premier ou pas ...
Re: QCM Ensam
Ça ne sert à rien de répondre à un énoncé imprécis.
Rédige l'énoncé complet. En plus c'est un QCM, donne la liste des choix.
(1,1) - N premier
(1,2) - N non premier
Rédige l'énoncé complet. En plus c'est un QCM, donne la liste des choix.
(1,1) - N premier
(1,2) - N non premier
Re: QCM Ensam
Bonjour;
M.Zygomatique a donné la solution a cet exercice:
Il y a des cas où est un nombre premier, comme par exemple si on a
est un nombre premier, comme par exemple si on a  qui donne
qui donne  et des cas où
et des cas où  n'est pas un nombre premier, comme par exemple si on a
n'est pas un nombre premier, comme par exemple si on a  qui donne
qui donne  .
.
En général on a:
^4 = (A^2)^2 + ((\sqrt 2 B)^2)^2)
^2 + ((\sqrt 2 B)^2)^2 + 2 A^2 (\sqrt 2 B)^2 - 2 A^2 (\sqrt 2 B)^2 = (A^2 + (\sqrt 2 B)^2)^2 - 2 A^2 (\sqrt 2 B)^2)
^2)^2 - (2AB)^2 = (A^2 + 2 B^2)^2 - (2AB)^2)
(A^2 + 2 B^2 + 2AB) = ((A-B)^2+B^2)((A+B)^2+B^2))
M.Zygomatique a donné la solution a cet exercice:
Il y a des cas où
En général on a:
Re: QCM Ensam
aymanemaysae a écrit:Bonjour;
M.Zygomatique a donné la solution a cet exercice:
Il y a des cas oùest un nombre premier, comme par exemple si on a
qui donne
et des cas où
n'est pas un nombre premier, comme par exemple si on a
qui donne
.
En général on a:
Bonjour,
Il me semble qu'on peut trouver un calcul plus simple....
Re: QCM Ensam
chaque facteur est une somme de carrés donc positifs ...
n est premier si et seulement si un seul des facteurs est 1 ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: QCM Ensam
zygomatique a écrit:
chaque facteur est une somme de carrés donc positifs ...
n est premier si et seulement si un seul des facteurs est 1 ...
1 ligne.... (en rajoutant un carré qui manquait).
ar1 = à rien, je suppose...
Re: QCM Ensam
Pseuda a écrit:zygomatique a écrit:
chaque facteur est une somme de carrés donc positifs ...
n est premier si et seulement si un seul des facteurs est 1 ...
1 ligne.... (en rajoutant un carré qui manquait).
ar1 = à rien, je suppose...
ou un germanophile ...

merci de la correction
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: QCM Ensam
Voici des liens qui traitent du même sujet.
http://www.ilemaths.net/sujet-a-quels-condition-a-4-4b-4-est-il-premier-247711.html
http://www.ilemaths.net/sujet-nombres-premiers-48607.html
http://www.ilemaths.net/sujet-a-quels-condition-a-4-4b-4-est-il-premier-247711.html
http://www.ilemaths.net/sujet-nombres-premiers-48607.html
Re: QCM Ensam
Bonjour;
je suis allé là où M.Razes nous a indiqué la solution, et je suis revenu avec çà (je l'ai rédigé pour le plaisir, vu qu'il n'y a plus mystère).
On a^2+B^2)((A+B)^2+B^2)) , donc
, donc
*) Si^2\ge4+(A-B)^2\ge4\\B^2+(A+B)^2\ge4+(A+B)^2\ge4\end {matrix}) ,
,
donc les deux facteurs de sont supérieurs ou égaux à
sont supérieurs ou égaux à  , donc
, donc  n'est pas un nombre entier naturel premier.
n'est pas un nombre entier naturel premier.
**) Si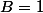 , donc on a
, donc on a ^2+1)((A+1)^2+1))
 si
si ^2+1\ge2\\(A+1)^2+1\ge10\end {matrix}) , donc
, donc  n'est pas un nombre entier naturel premier.
n'est pas un nombre entier naturel premier.
 si
si 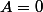 , on a
, on a  , donc
, donc  n'est pas un nombre entier naturel premier.
n'est pas un nombre entier naturel premier.
 si
si 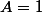 , on a
, on a  , donc
, donc  est un nombre entier naturel premier.
est un nombre entier naturel premier.
***) si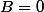 et
et 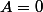 donc
donc  , donc
, donc  n'est pas un nombre entier naturel premier.
n'est pas un nombre entier naturel premier.
****) si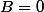 et
et 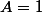 donc
donc  , donc
, donc  n'est pas un nombre entier naturel premier.
n'est pas un nombre entier naturel premier.
*****) si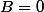 et
et 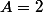 donc
donc  , donc
, donc  n'est pas un nombre entier naturel premier.
n'est pas un nombre entier naturel premier.
Conclusion: n'est pas un nombre entier naturel premier sauf si
n'est pas un nombre entier naturel premier sauf si  .
.
je suis allé là où M.Razes nous a indiqué la solution, et je suis revenu avec çà (je l'ai rédigé pour le plaisir, vu qu'il n'y a plus mystère).
On a
*) Si
donc les deux facteurs de
**) Si
***) si
****) si
*****) si
Conclusion:
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
