3^cosx + 3 ^ (cos(pi - x) +1) < 2 racine de 3
résoudre l équation....
En faite je l ai derivee en tant que fonction et j ai effectué le tableau de variation mais cela n etait suffisant...
Que puis-je faire pr resoudre cette equation merci d avance...
Résoudre une Equation (concours ensam 2015)
7 messages
- Page 1 sur 1
Re: Résoudre une Equation (concours ensam 2015)
par anthony_unac » 30 Juil 2016, 14:09
Solution graphique pourquoi pas ...
Alors allons y dessinons les courbes représentatives des deux fonctions figurant dans l'inéquation et observons ce qu'il se passe.
Solution algébrique, et si on essayait de mettre en facteur})
... allez c'est jouable ! 
Après on pourrait peut être faire tomber)
au sol car il est bien trop haut perché en l'état.
Alors allons y dessinons les courbes représentatives des deux fonctions figurant dans l'inéquation et observons ce qu'il se passe.
Solution algébrique, et si on essayait de mettre en facteur
Après on pourrait peut être faire tomber
Re: Résoudre une Equation (concours ensam 2015)
par anthony_unac » 30 Juil 2016, 14:28
Quelques essais m'ont permis d'y voir plus clair.
Sur le plan algébrique, mettre en facteur ne mène à rien (faute d'un signe) alors vous pouvez en revanche poser })
Sur le plan algébrique, mettre en facteur
Re: Résoudre une Equation (concours ensam 2015)
par aymanemaysae » 30 Juil 2016, 15:29
Bonjour;
} + 3^{\cos(\pi-x)+1}<2\sqrt 3 \Rightarrow 3^{\cos(x)} + 3*3^{-\cos(x)}<2\sqrt 3)
} + 3 <2\sqrt 3*3^{\cos(x)} \Rightarrow 3^{2\cos(x)} -2\sqrt 3*3^{\cos(x)} + 3 < 0)
} - \sqrt 3)^2 < 0)
, donc l'inéquation n'a pas de solution .
Si au contraire on a :
} + 3^{\cos(\pi-x)+1} \le 2\sqrt 3 \Rightarrow 3^{\cos(x)} + 3*3^{-\cos(x)} \le 2\sqrt 3)
} + 3 \le 2\sqrt 3 *3^{\cos(x)} \Rightarrow 3^{2\cos(x)} -2\sqrt 3 * 3^{\cos(x)} + 3 \le 0)
} - \sqrt 3)^2 \le 0 \Rightarrow (3^{\cos(x)} - \sqrt 3)^2 = 0)
} - \sqrt 3 = 0 \Rightarrow 3^{\cos(x)} = \sqrt 3)
 \ln(3) = \frac{1}{2} \ln(3) \Rightarrow \cos(x) = \frac{1}{2})
 = \cos(\frac{\pi}{3}) \Rightarrow x = \pm \frac{\pi}{3} + k2\pi)
avec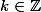 
.
Si au contraire on a :
Modifié en dernier par aymanemaysae le 30 Juil 2016, 16:30, modifié 1 fois.
Re: Résoudre une Equation (concours ensam 2015)
par samoufar » 30 Juil 2016, 16:15
Bonjour,
Ce n'est pas bien méchant, mais je crois que c'est plutôt
} + 3*3^{-\cos(x)}<2\sqrt 3\Rightarrow 3^{2\cos(x)} + 3 <2\sqrt 3 \cdot 3^\cos(x))
(en notant bien que }> 0)
pour justifier la conservation de l'inégalité dans ce sens).
À part ça le résultat est le même
aymanemaysae a écrit:
Ce n'est pas bien méchant, mais je crois que c'est plutôt
À part ça le résultat est le même
Re: Résoudre une Equation (concours ensam 2015)
par aymanemaysae » 30 Juil 2016, 16:31
Bonjour;
Merci M.Samoufar, je viens de rectifier mon erreur.
Encore une fois, Merci.
Merci M.Samoufar, je viens de rectifier mon erreur.
Encore une fois, Merci.
Re: Résoudre une Equation (concours ensam 2015)
par Maneeeel » 30 Juil 2016, 23:13
Merci énormément...
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :