Propriété des limites d'une fonction impaire

[chalelu]

Bonsoir à tous,

Je viens vers vous, car j'ai une question concernant les limites en deux points (opposées) d'une fonction impaire. La question est la suivante :

Si la fonction est impaire, et si , alors .
Vrai ou faux ? Merci par avance

Bonne soirée à tous,
Chalelu

[infernaleur]

Salut graphiquement comment tu peux voir si une fonction est impaire ?

[chalelu]

Salut graphiquement comment tu peux voir si une fonction est impaire ?

Graphiquement la fonction impaire, est une fonction qui est symétrique par rapport à l'origine.
C'est pour cela que je me posais cette question ...

[infernaleur]

Bonsoir à tous,

Je viens vers vous, car j'ai une question concernant les limites en deux points (opposées) d'une fonction impaire. La question est la suivante :

Si la fonction est impaire, et si , alors .
Vrai ou faux ? Merci par avance

Bonne soirée à tous,
Chalelu

, alors sa aurait plus de sens de se poser cette question alors ?

[chalelu]

Bonsoir à tous,

Je viens vers vous, car j'ai une question concernant les limites en deux points (opposées) d'une fonction impaire. La question est la suivante :

Si la fonction est impaire, et si , alors .
Vrai ou faux ? Merci par avance

Bonne soirée à tous,
Chalelu

, alors sa aurait plus de sens de se poser cette question alors ?

Effectivement, si on prend par exemple la fonction on a :


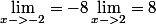
Mais on sait qu'un exemple ne permet pas une généralisation d'une propriété, c'est pour cela que je me pose cette question

[infernaleur]

Oui tu as raison,
bon on va supposer f continue et définie sur R pour pas qu'on ait de problème de continuité etc ...

Bon on veut montrer cette "propriété"
Soit f une fonction de R dans R et continue sur R et soit a,b appartenant à (c'est-à-dire ce sont des réels qui peuvent valoir +l'infini).
Si la fonction est impaire, et si , alors

Tu peux essayer un changement de variable pour faire apparaître ton hypothèse sur la parité .

[chalelu]

Oui tu as raison,
bon on va supposer f continue et définie sur R pour pas qu'on ait de problème de continuité etc ...

Bon on veut montrer cette "propriété"
Soit f une fonction de R dans R et continue sur R. Soit a,b appartenant à (c'est-à-dire ce sont des réels qui peuvent valoir +l'infini).
Si la fonction est impaire, et si , alors

Tu peux essayer un changement de variable pour faire apparaître ton hypothèse sur la parité .

Ah je viens de comprendre votre raisonnement, effectivement cette propriété est fausse pour une fonction impaire, mais elle est vraie pour une fonction paire n'est-ce-pas ?

[infernaleur]

Non pourquoi est-ce que elle serait fausse ? Et je n'ai pas vraiment fait de raisonnement à part t'avoir donné une idée de démo.

( [edit] J'ai changé un peu le contenu de mon précédent post)

[infernaleur]

Ah pardon je viens de comprendre tu parles de la propriété que tu as énoncé plus haut ? Oui en effet tu as raison elle est vraie pour une fonction paire (je pensais que tu parlais de la propriété que j'ai écrite plus haut).
Peux-tu le démontrer ?

[chalelu]

Ah pardon je viens de comprendre tu parles de la propriété que tu as énoncé plus haut ? Oui en effet tu as raison elle est vraie pour une fonction paire (je pensais que tu parlais de la propriété que j'ai écrite plus haut).
Peux-tu le démontrer ?

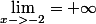
Oui je parlais de mon premier post. Bah la fonction est symétrique par rapport à l'axe des ordonnées ce qui implique : alors

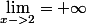
[infernaleur]

Ah pardon je viens de comprendre tu parles de la propriété que tu as énoncé plus haut ? Oui en effet tu as raison elle est vraie pour une fonction paire (je pensais que tu parlais de la propriété que j'ai écrite plus haut).
Peux-tu le démontrer ?

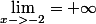
Oui je parlais de mon premier post. Bah la fonction est symétrique par rapport à l'axe des ordonnées ce qui implique : alors

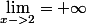
Mais sans utiliser le graphe tu peux raisonner comme suite :
Si tu pose x=-t,
quand x tend vers -2 bha t tend vers 2, donc par composition de limite ,