Bonsoir,
Voici mon problème :On se place dans

avec

grand. Soit

très petit devant

. Je possède

relations affines de la forme
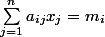
avec
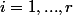
. Je pose

le sous-espace affine de

défini par ces relations. Je souhaite calculer une projection orthogonale d'un point de

sur cet espace.
On a M de dimension

car déterminé par

relations. (Je suppose que le calcul final de la projection consistera à inverser un système linéaire déterminé par une matrice de taille

dont il faut déterminer les coefficients).
Voici ma solution :Soit
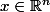
que l'on souhaite projeter sur

.
1- On calcule un point
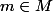
qui fera office d'origine à translation près. On le fait en se fixant

coordonnées arbitraires, on les injecte dans les relations affines. Les

dernières coordonnées sont alors obtenues en inversant un système linéaire de taille

.
2-On calcule une base de
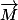
, la direction de

. Pour cela, on fixe
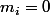
pour avoir les équations linéaires caractérisant
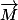
puis on échelonne le système. On trouve alors naturellement une base de

vecteurs en fixant des coordonnées à

. Notons cette base
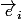
.
3- On orthonormalise cette base à l'aide de l'algorithme de Gram-Schmidt.
4- On translate

par
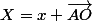
5- On projette

sur
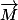
par la formule
 = \sum_{i=1}^{n-r}(X, \vec{e}_i)\vec{e}_i)
. (Avec
)
le produit scalaire).
6- On applique la translation dans l'autre sens pour obtenir le résultat souhaitée :
 = \pi_{\vec{M}}(X) + \vec{OA}) Voici mes questions :
Voici mes questions :Est-ce que mon algorithme est bon ?
Mon but étant de programmer cet algorithme, je souhaite estimer sa complexité et savoir s'il n'y en a pas un meilleur. la valeur de

a-t-elle un impact notable sur la complexité (si je prend plutôt

proche de

) ? Qu'en pensez-vous ?
En vous remerciant,
Rhaegar
