Projection orthogonale sur un Hilbert

par **ludo56** » 14 Mai 2009, 08:40

Bonjour,
Soit

un espace de Hilbert et

un sous espace vectoriel de H. J'ai sous la main deux bouquins, le premier disant que l'on a la décomposition orthogonale

sans conditions particuliere sur

, tanqis que l'autre dit que

est un sous espace vectoriel fermé.Alors qu'en est t'il ?
Merci d'avance!

par **L.A.** » 14 Mai 2009, 09:53

Bonjour.

Dans mon cours, il faut bien que F soit fermé.
Après je n'ai pas de contre-exemple sous la main si ce n'est pas le cas.

par **legeniedesalpages** » 14 Mai 2009, 10:00

Salut,

Dans le premier bouquin, il doit être question de supplémentaire algébrique,
dans le second on doit parler de supplémentaire topologique.

par **L.A.** » 14 Mai 2009, 10:09

Tiens ben je crois avoir trouvé :

si H=(C[0,1],||.||2), et F est le noyau de u |-> u(0) (non fermé).
alors on a l'orthogonal de F = {0}

par **yos** » 14 Mai 2009, 10:09

Si F est pas fermé, il est pas complet et par suite

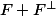
non plus (additionner une suite de Cauchy non convergente de F et une suite constante de

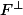
). Or H est complet.
Argument à vérifier.

par **ludo56** » 16 Mai 2009, 16:37

Merci a tous ! Effectivement je pense que l'hypothèse fermé est necessaire!