Projecteurs orthogonaux spectre de leurs composées

[VincentVega]

Bonjour à tous,
J'ai besoin d'aide sur une question:
"Soient p et q des projecteurs orthogonaux. Montrer sp(p°q) inclus dans [0,1]"

[GaBuZoMeu]

Bonjour,

Soit un vecteur propre unitaire de 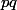. Tu peux introduire un vecteur unitaire tel que . Quelle est alors la valeur propre associée à ?

[VincentVega]

Je ne vois pas très bien comment séparer u dans le produit<u,v>*v
j'ai pensé aux identités de polarisation mais même problème...
(je précise qu' on est dans E préhilbertien réel)

[GaBuZoMeu]

Que veux-tu dire par "séparer " ? Je ne comprends pas.
On peut mettre à part le cas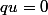 . Si alors on peut poser et on a bien puisque est un projecteur orthogonal.

[VincentVega]

Je veux retrouver la forme f(x)=lambda*x avec lambda valeur propre de f et x vecteur propre de f
Ce qui va me permettre de trouver la valeur propre associée à u.

[GaBuZoMeu]

Puisque est vecteur propre de 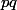, tu sais que où est la valeur propre associée à .
Tu sais que et tu sais que est un projecteur orthogonal. Avec ça, tu peux trouver .

[VincentVega]

J'obtiens p(<u,v>*v)=lambda*u

ie lambda=p(<u,v>*v)/u=<u,v>p(v)/u

je ne vois pas comment conclure

[GaBuZoMeu]

Oh la ! Diviser par un vecteur, ce n'est pas top !

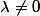Voyons, si est un projecteur orthogonal et si avec vecteur unitaire et , ne peux-tu pas exprimer à partir de et (sans diviser par un vecteur !) ?
Indication : on a donc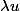 orthogonal à .

[VincentVega]

en utilisant <λu, w-λu>=0
j'obtiens λ=<u,w>/IIuII²

(j'en profite pour vous remercier du temps que vous m'accorder)

[GaBuZoMeu]

Je rappelle que .
Alors, as-tu pu conclure ?

[VincentVega]

On a λ=<u,w>

Est ce que Cauchy-Schwarz fonctionne ?
avec I<u,w>I<=IIuII*IIvII=1

[GaBuZoMeu]

Qui est w dans l'histoire ?

[VincentVega]

q(u)

[GaBuZoMeu]

Et donc ?

[VincentVega]

On a bien λ<=1
Quelque chose m'échappe?

[GaBuZoMeu]

Je ne vois pas ton argument.
Peux-tu l'expliciter, en entier ?

[VincentVega]

λ=<u,w>
=<u,q(u)>
Or q(u)=<u,v>*v
donc
λ=<u,v>*<u,v>
<=IIuII² *IIvII²=1

[GaBuZoMeu]

Un peu de phrase ne serait pas mal.
Ne pas oublier de dire que \lambda est positif ou nul.
Et ne pas oublier de traiter à part le cas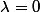 (il y a un moment où on fait une division par ).

[VincentVega]

Très bien
Merci beaucoup pour votre aide!