Produit fibré
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Julien8
- Membre Naturel
- Messages: 39
- Enregistré le: 03 Nov 2012, 01:38
-
 par Julien8 » 10 Déc 2014, 23:45
par Julien8 » 10 Déc 2014, 23:45
Bonsoir à tous, je suis bloqué sur quelque chose..
J'aimerais montrer que dans le diagramme suivant, le produit fibré est bien G/UnV
Auriez-vous une idée ?

Merci beaucoup et bonne fin de soirée.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Déc 2014, 23:52
par Ben314 » 10 Déc 2014, 23:52
Salut,
Tu es dans une catégorie particulière (groupes,e.v., topologie...) ?
EDIT : en fait, vu le produit UV en bas à droite, ça doit pas être des espaces topo. ou des e.v.... :hum:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Julien8
- Membre Naturel
- Messages: 39
- Enregistré le: 03 Nov 2012, 01:38
-
 par Julien8 » 10 Déc 2014, 23:55
par Julien8 » 10 Déc 2014, 23:55
Ce sont des groupes !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Déc 2014, 00:29
par Ben314 » 11 Déc 2014, 00:29
Si

est un groupe et

[rep.
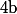
] un morphisme de

dans

[resp.

] tel que le diagramme avec

,

,

et

commute.
Pour tout

, on a par hypothèse
UV=b(h)UV)
donc
=a(h)uv)
avec

et

.
Pour définir le morphisme
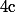
de
)
, on cherche les

tel que
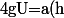U=a(h)uU)
et
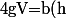V=a(h)uV)
et les solutions sont exactement les
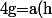uw)
avec

qui forment une unique classe dans
)
ce qui montre que la seule valeur possible pour
)
est
=a(h)u(U\cap V))
d'où l'unicité de l'application
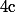
.
Ensuite, il est clair (=j'ai la flemme de vérifier... :zen:) que cette application
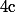
est bien un morphisme de groupe.
D'où le résultat.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Julien8
- Membre Naturel
- Messages: 39
- Enregistré le: 03 Nov 2012, 01:38
-
 par Julien8 » 11 Déc 2014, 00:47
par Julien8 » 11 Déc 2014, 00:47
Je médite encore un peu sur les détails (genre d'où sortent les petit u et v) mais merci beaucoup, c'est super.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités

