Problème sur les fractions rationnelles

[jonses]

Bonjour tout le monde,

J'ai essayé dernièrement de faire un exercice sur les fractions rationnelles. Comme, j'étais bloqué, j'ai regardé la correction, mais même la correction me posait des soucis. C'est pourquoi je poste ce message pour que je puisse trouver des explications.

Voici l'énoncé de l'exercice : (w_k signifie w indice k)

On pose w_k = e^(2ik;)/n) avec k un entier tel que (n-1) ;) k ;) 0, et n;) 2
Réduire au même dénominateur :

F=1/(X-w_0) + 1/(X-w_1) + ... + 1/(X-w_(n-1))

Voici la correction :

La réduction au même dénominateur de F s'écrit : F= P/(X^n -1) avec deg P< n (A)
Pour tout entier k tel que (n-1) ;) k ;) 0,
P(w_k)/n*w_k^(n-1) = 1 [C'est cette égalité que je n'arrive pas à saisir] (B)

donc P(w_k) - n*w_k^(n-1) = 0
Puisque P - n*X^(n-1) appartient à l'ensemble des polynômes de R[X] de degré inférieur à (n-1) et possède n racines, c'est donc le polynôme nul.
Finalement, F= (n*X^(n-1))/(X^n -1)

Si quelqu'un peut m'expliquer comment on est passé de la ligne (A) à la ligne (B), je le remercie d'avance.

[adrien69]

Salut
C'est un truc classique sur les décompositions en éléments simples. Regarde dans ton cours comment on calcule les coeffs de la décomposition d'une fonction rationnelle à pôles simples. Si tu ne comprends toujours pas je t'expliquerai en détail.

[jonses]

Merci pour ta réponse. J'ai essayé de refaire l'exercice en revoyant le cours comme tu me l'as dit, mais je n'y arrive toujours pas.

[adrien69]

En fait c'est parce qu'il y a une propriété générale qui existe et qui te donnait la formule directement que je t'ai demandé de vérifier. Mais si tu ne l'as pas refaisons-le à la main.

On a

Donc d'après Leibniz.

D'où le résultat.

[jonses]

Merci beaucoup, ça m'a fait rappeler une astuce qui mène aussi à la réponse.

Je me permets de la détailler pour être sûr de sa validité :

Déjà, soit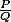 le représentant irréductible d'une fraction rationnelle (P et Q sont des polynômes qui n'ont pas de racines en commun). Et soit "a" un pôle de la fraction rationnelle.
On peut écrire :

avec U et G des polynômes qui n'ont pas de racine en "a".
On a alors k + (X-a)G = donc k =

mais comme Q = (X-a)U on a Q' = (X-a)U' + U d'où Q'(a)=U(a)

Ainsi (1)


On utilisant la relation (1) on peut résoudre le problème :

tel que P et X^n -1 n'aient pas de racines en commun

La décomposition en éléments simple donne


Donc on a d'après la relation (1) :

Or d'où
Puis le résultat

[adrien69]

Voilà, c'est de cette formule que je parlais. Si tu la connais c'est bien. Mais comme tu vois, on peut faire sans.

[jonses]

En tout cas, merci beaucoup ! Sans ton aide, j'aurais pas eu le déclic qui m'a fait rappeler tout ça.