\exp(-Px) *\cos(Wx)
J'ai du mal trouvé la primtive de cette fonction.
Merci de me répondre.
Problème de primitive d'un produit de deux fonctions
9 messages
- Page 1 sur 1
Re: Problème de primitive d'un produit de deux fonctions
par anthony_unac » 16 Nov 2019, 21:27
Salut,
C'est difficile de comprendre en l'état peux tu nous expliquer ... j imagine que x est la variable
C'est difficile de comprendre en l'état peux tu nous expliquer ... j imagine que x est la variable
Re: Problème de primitive d'un produit de deux fonctions
par Yezu » 16 Nov 2019, 21:59
Salut,
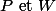sont des réels, des fonctions de x, ou ?
Re: Problème de primitive d'un produit de deux fonctions
par aymanemaysae » 16 Nov 2019, 22:44
Bonsoir;
Pour ma part ; j'essaierai tout d'abord de trouver une primitive de exp(px) exp(iwx) .
Pour ma part ; j'essaierai tout d'abord de trouver une primitive de exp(px) exp(iwx) .
Re: Problème de primitive d'un produit de deux fonctions
par aymanemaysae » 17 Nov 2019, 07:49
Bonjour ;
De même , une double intégration par parties fera l'affaire .
De même , une double intégration par parties fera l'affaire .
Re: Problème de primitive d'un produit de deux fonctions
par aymanemaysae » 17 Nov 2019, 12:13
L'avantage de la première méthode c'est qu'elle te donnera une primitive de exp(px)cos(wx) et une primitive de exp(px)sin(wx) en bonus .
Re: Problème de primitive d'un produit de deux fonctions
par mathelot » 17 Nov 2019, 12:39
Bonjour,
avec l'exponentielle complexe:
dx)
dx)
x}}{-P+iW}+\dfrac{e^{(-P-iW)x}}{-P-iW} \right))
)
e^{iWx}}{P^2+W^2}+\dfrac{(-P+iW)e^{-iWx}}{P^2+W^2} \right))
l'intégrale est réelle donc égale à sa partie réelle:
} e^{-Px} 2 \, \Re\left( -P-iW)e^{iWx}\right))
+Wsin(Wx)\right))
avec l'exponentielle complexe:
l'intégrale est réelle donc égale à sa partie réelle:
Re: Problème de primitive d'un produit de deux fonctions
par aymanemaysae » 17 Nov 2019, 15:38
Une autre version de la solution de Mathelot .
On a :x})
;
donc si\ne (0 ; 0))
alors une primitive de x})
estx}}{-p + iw}+k)
avec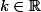 
.
On a :x}}{-p + iw} = \dfrac{-p-iw}{p^2+w^2}e^{(-p+iw)x})
e^{iwx})
(cos(wx) + isin(wx)))
 + w sin(wx) + i(-p sin(wx)-w cos(wx))))
.
Comme + i sin(wx)) = e^{-px} cos(wx) + i e^{-px} sin(wx))
alors une primitive de)
est  + w sin(wx) + k)
avec 
et une primitive de)
est  - w cos(wx) + k)
avec .
Le cas = (0 ; 0))
est trivial :  = 1)
qui admet pour primitive 
avec .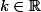
Il te reste Monsieur ZenZone d'essayer d'utiliser la double IPP .
On a :
donc si
On a :
Comme
alors une primitive de
et une primitive de
Le cas
Il te reste Monsieur ZenZone d'essayer d'utiliser la double IPP .
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :