Equation deux deux fonctions (euclidienne?)

[evrard]

HA tout d'abord je trouve l'idée de ce forum génial! Je suis un peu desespéré, j'essaye de comprendre mes maths seul, et je n'y arrive pas du tout!
Je suis en première année de fac d'économie et gestion!!
Mon problème est le suivant! je ne comprends pas comment on peut divisier A par B si ce sont des fonctions! je relis mon cour, et surtout l'exemple, je ne comprend pas la procédure!

je dois diviser A(x)=2x^4 + 5x² - 10x + 1
par B(x) = 2x² - 5x + 5

Je ne cherche pas a voir le resultat, c'est vraiment comment on doit s'y prendre, car j'aurais mes premiers controles a la mi octobre... et j'aimerais pouvoir me debrouiller seul!
Si quelqu'un se sent capable de m'expliquer , et surtout veut bien le faire, je lui en serais très reconnaissant! Merci beaucoup

[LN1]

Bonjour, en remettant tout en place, il me semble qu'il s'agit d'une division euclidienne pour deux polynômes et non d'une division pour deux fonctions.

Il s'agit d'une opération qui s'apparente à la division euclidienne entre deux entiers naturels
division euclidienne de A par B : il faut trouver deux entiers naturels q et r tels que
A = Bq + r avec r < B

On crée une autre opération sur les polynomes et on lui donne le même nom à cause des ressemblence entre les deux
division euclidienne de A par B : il faut trouver deux polynômes q et r tels que
A = Bq + r avec degré de r < degré de B

la ressemblance est telle que l'on peut aller jusqu'à poser une division comme en primaire.

Pour te laisser travailler, je prends volontairement un autre exemple: division euclidienne de par
le degré de B est 2, le degré de r doit être 1, ou 0 ou - oo

en combien de fois , il y va fois

que j'ôte à , reste

on recommence
en combien de fois , il y va 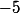fois

que j'ôte à -, reste

donc
A = B(x - 5) + 22x - 28
q = x - 5
r = 22x - 28

(en fait, tout mon baratin , c'est parceque je ne peux pas poser correctement la division ici)
attention, une erreur de calcul n'est pas improbable

[Anonyme]

donc je fais en x^4, combien de fois de x²?, il y a 2x² fois
*2x²(x²-5x+5)= 2x^4-10x^3+10²
(2x^4-5x²-10x+1) - (2x^4-10x^3+10x²)
= -10x^3-15x²-10x+1

donc je fais en -10x^3 combien de fois de x²?, il y a -5x fois
*-5x (2x²-5x+5)= -10x^3+25x²-25x
(-10x^3-15x²-10x+1) - (-10x^3+25x²+25x)
=-35x²+15x+1

et après comment je fais? je suis bloqué non?

[evrard]

désolé j'ai oublié de m'identifié :hum:

[LN1]

Non,

1) tu commences par te tromper sur le premier polynôme est-ce
ou

2) tu te trompes dans le deuxième polynôme: est-ce
ou

si tu cherches à diviser par
tu dois regarder les termes de poids fort : d'un côté et 2x² de l'autre.
en , combien de fois 2x² il y va x² fois
etc...


au bout de deux étapes, tu obtiens comme reste 12,5x² - 22,5x + 1 dont le degré est encore trop grand : il faut donc continuer
en 12,5x² combien de fois 2x² etc.

[evrard]

J'ai eu mon TD ce matin! J'ai compris entièrement l'opération merci beaucoup! L'explication du cour était très abstraite, mais riende mieux que des démonstration! merci beaucoup en tout cas