Problème de logarithme

[Hichiro]

Bonjour je tente de comprendre mes exercice de logarithme mais j'ai de nombreux problème :mur:

Par exemple cet exercice:

1) 1 000 000^x = 1 000^x + 2

1 000 000 = 10^6 -> log(6^x)
1000 = 10^3 -> log(3^x)

log(6^x) = log(3^x) +2

bloquer ici..


2)
(log(27x) / log4) = log(x²) / log2)
(log(27x) / 2log2) = log(x²) / log2)
log2 * log(27x) = 2log2 * log(x²)
log(27x) = 2 * log(x²)
log(27x) = 2log(x²)
log (27x) = log(x^4)
3 log(9x) = 2 log(2x)
et après?

3)

3^(x+2) + 9(x-1) = 1458
3^(x)*6+((3³)^(x-1) = 1458
3^(x) + ((3³)^(x-1)) = 1458
3^(x) + ((3^(3x))*(-9)) = 1458
18^(x) + (-27^(3x)) = 1458
ensuite .. (oui je suis mauvais)

4)

2^x + 2^(x+1) + 2^(x+2) + 2^(x+3) = 3^x + 3^(x+1) + 3^(x+2) + 3^(x+3)
avez vous une formule à me proposer?

J'ai bien lu la charte et ne demande pas la réponse mais que on m'aiguille (formule, remarque, erreur commise,..) si je pose plusieur exercice c'est du fait que je suis en étude de plusieurs matière en même temps ..


Merci beaucoup

[chan79]

Bonjour je tente de comprendre mes exercice de logarithme mais j'ai de nombreux problème :mur:

Par exemple cet exercice:

1) 1 000 000^x = 1 000^x + 2

poser
Trouver X et ensuite, penser aux logarithmes

[Hichiro]

je suppose que on remet tout du même coter comme ceci:
10^{6x}-x-2=0
mais
après que faire du 10^{6x} ?

[Archytas]

je suppose que on remet tout du même coter comme ceci:
10^{6x}-x-2=0
mais
après que faire du 10^{6x} ?

Exprime le aussi en fonction de X ! Et ne confond pas x et X !

[Hichiro]

Merci, si je comprend bien je me retrouve avec:

10^{6x}- 10^{3x} -2 = 0

on pose 10^{3x} = X

donc: 2X - X - 2 = 0

X - 2 = 0
10^{3x} - 2 = 0

Mais que faire pour trouver x ?

[ampholyte]

Bonjour,

Tu peux te souvenir que :

[Hichiro]

je crois mettre tromper aussi.

10^{6x}- 10^{3x} -2 = 0

on pose 10^{3x} = X

donc: X² - X - 2 = 0

[ampholyte]

Il faut donc résoudre une équation du second degré.

Une fois les solutions trouvé, tu peux réecrire que :



Il te suffira alors de prendre ln pour trouver x.

Tu retrouves la définition du log (logarithme décimal et non logarithme népérien) =).

D'où :

et

[Hichiro]

J'ai fait le delta et trouver x1, x2 ( S={1 ; 2} )

par contre je ne comprend pas ta solution proposé.. J'ai essayer de la résoudre mais j'ai syntax error à la calculatrice

[Black Jack]

(10^6)^x = (10^3)^x + 2

Poser (10^3)^x = y ---> y > 0

y² = y + 2
y² - y - 2 = 0

y = (1 +/- 3)/2

y = 2 est la seule solution (puisque y doit être > 0)

(10^3)^x = 2
x.log(10^3) = log(2)

x = (1/3).log(2)
Le log est ici décimal (base 10)

:zen:

[Hichiro]

merci, j'ai du mal à comprendre comment tu passe de
x.log(10^3) = log(2)
à:
x = (1/3).log(2)

[chan79]

J'ai fait le delta et trouver x1, x2 ( S={1 ; 2} )

par contre je ne comprend pas ta solution proposé.. J'ai essayer de la résoudre mais j'ai syntax error à la calculatrice

tu devrais revoir le calcul

[Hichiro]

oui S={-1;2} j'ai oublier le moins en fesant le calcul

[fibonacci]

bonjour;

[Black Jack]

merci, j'ai du mal à comprendre comment tu passe de
x.log(10^3) = log(2)
à:
x = (1/3).log(2)

x.log(10^3) = log(2)
Avec des log décimaux ---> log(10^3) = 3

3.x= log(2)

x = (1/3).log(2)

Il n'est nul besoin ici d'utiliser des logarithmes népériens, c'est inutile surtout quand on est amené à manipuler des puissances de 10. Le log décimal est alors plus indiqué.

Ce qui ne signifie pas qu'on ne peut pas utiliser le ln, mais c'est sans réel intérêt.

:zen:

[deltab]

Bonjour.

@Hichiro

Pour 2)
(log(27x) / log4) = log(x²) / log2)
d'où (log27)/(2log2)+logx/(2log2)=2logx/log2 et (log27)/2+logx/2=2logx
tu as alors une équation linéaire en logx, i.e. en posant X=logx, l'équation devient une équation linéaire en X

Pour 3)
Il manque le signe ^ dans 9(x-1), ce serait plutôt 9^(x-1) qu'il fallait écrire dans la 1ère ligne et c'est 3² et non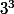 dans la deuxième
Avec ces rectifications, on obtient (même démarche que pour 1)):


En posant , l'équation devient une équation du second degré en X

Pour 4)



Je n'en dis pas plus.

[Black Jack]

2)

log(27x) / log4 = log(x²) / log2
log(27x) / (2.log2) = log(x²) / log2
log(27x) = 2.log(x²)
log(27x) = log(x^4)

x doit être > 0

27x = x^4
x³ = 27
x = 3
*****
:zen: