Problème de géométrie - triangle equilatéral

[nico_maths63]

Bonjour à tous,

J'ai besoin de votre aide pour résoudre un petit problème de mathématiques. Voilà, il s'agit de retrouver les coordonnées des sommets d'un triangle équilatéral de côté "c", sachant que ces sommets sont situés sur trois droites (pas nécessairement concourantes en un point et pas non plus des droites spécifiques : ce n'est pas des médianes, ni bissectrices...) dont je connais les équations. Il est clair que j'arrive à obtenir 6 équations pour 6 inconnus mais je n'arrive pas à extraire une solution analytique de ce système d'équation. Je suis parti du fait que les sommets sont sur les trois droites (donc ils vérifient les équations de la droite à laquelle ils appartiennent) ce qui donne 3 équations, et que la longueur du segment qui relie chaque sommet est constante et égale à la longueur du côté du triangle "c" ce qui donne 3 équations supplémentaires (mais quadratique car c'est l'écriture de la norme du vecteur) du coup je n'arrive pas a obtenir de solution....Est-ce que quelqu'un pourrais m'aider??

merci d'avance

Nicolas

[dudumath]

si tu fais l'intersection 2 à 2 des droites, tu obtiendras tes 3 points

[Ben314]

Salut,
A moins que je ne me gourre, j'ai l'impression qu'il y a en général une infinité de solutions : Tu veut construire un triangle équilatéral de sommet A, B et C respectivements situés sur des droites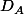 , et connues.
On suppose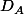 et sécantes en un point O.
Commence par prendre deux points distincts et au hazard puis construit 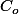tel que le triangle soit équilatéral (deux choix possibles).
L'image par une homothétie de centre O et de rapport quelconque te fournit un triangle équilatéral dont les sommets et sont respectivement sur 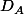et . Reste à trouver le bon rapport pour que soit sur .
Si l'on regarde l'ensemble des images de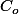 par les différentes homothéties de centre O, on obtient évidement la droite (en supposant que ) et, si elle n'est pas parallèle à elle coupe cette dernière en un unique point C.
Il n'y a plus qu'à tracer les intersection A [et B] de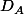 (resp. TEX]D_B[/TEX]) de la parallèle à (resp. ) passant par C pour avoir un triangle solution.

Conclusion, modulo 1 ou 2 exeptions, on peut construire exactement deux tels triangles avec une base (AB) parallèle à n'importe quelle direction fixée d'avance.

Edit, je pense que, là ou tu te plante, c'est que, pour traduire que ABC est équilatéral, on écrit que AB=BC=CA et que ça ne fait que deux équations et pas trois. Cela explique que tu ait un degrés de liberté dans les solutions (par exemple le choix de la direction de (AB)).
Tu pourait aussi imposer une position particulière au point A sur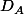 puis trouver C et regardant l'intersection de et de l'image de par une rotation d'angle centrée en A...

P.S. Vive la "vrai" géométrie, au chiotte les équations... :marteau:

[nico_maths63]

Bonjour Ben314,

Merci pour ta réponse. Effectivement il y a une infinité de solutions c'est à dire plusieurs triangles équilatérales dont les sommets sont situés sur ces droites. Néanmoins, il y en a qu'un seul qui a le côté de le bonne longueur, en tout cas c'est ce que j'ai l'impression.

Qu'en penses-tu??

Merci

Nicolas

[Ben314]

Désolé : effectivement, j'avais (encore) lu to post trop rapidement et je n'avais pas vu que le coté du triangle équilatéral était fixé : cela fait une équation de plus et il semblerait raisonable qu'il n'y ait qu'un nombre fini de solutions (par exemple 0 dans certain cas)...

Si j'ai un peu de temps, je regarde...

[Ben314]

Si tu prend un segment [AB] de longueur c fixée tel que et puis que tu construit C tel que ABC soit équilatéral direct, le lieu du point C lorsque le segment prend toutes les positions possibles est une éllipse ( d'axes les bissectrices de 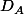et ). Idem avec une autre élipse si on construit C tel que ABC soit équilatéral indirect.
La droite peut couper chacune des élipses en 2 points, donc, au max, il y a quatre solutions.
Ce point de vue permet de voir que tu as fortement intérêt à chercher indépendement les triangles directs et indirects (2 sol. au max dans chaque cas => équation seulement du second degrés)