Bonjour à tous...
J'ai un petit souci de compréhension dans la démonstration de la commutativité de la multiplication dans
.
Rappels :
(on dit que 0 est un élément absorbant)
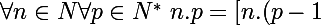]+n$$)
La loi
ainsi définie est associative, commutative et distributive par rapport à l'addition.
Voici la démo de la commutativité :
Notons que l'on a toujours
si
ou si
. Montrons que
par récurrence sur
.
Si
ou
,
ou
est nul et l'assertion est triviale.
Au rang
, et si
avec
, on écrit :
+n=(p-1)n+n=(p-1)(n-1)+(p-1)+n$$)
+p=(n-1)p+p=(n-1)(p-1)+(n-1)+p$$)
Où
représente le prédecesseur de
de sorte que l'égalité entre ces deux quantité provienne de l'égalité :
+n=(n-1)+p)
.
Ma question concerne le lancement de cette récurrence (puisque j'ai compris le reste) :
que veut dire "par récurrence sur 
", en d'autres termes, d'où sort ce 
et pourquoi le définit-on à partir de 
?
