Problème de calcul de probabilité

[Alex060496]

Bonjour à tous,

Je cherche à estimer une probabilité mais je manque un peu de méthode et j'ai perdu beaucoup de compétence en probabilité. J'espère que l'un de vous pourra m'éclairer sur la manière de résoudre mon problème. En voici un version simplifiée et épurée :

J'ai un paquet de 10 cartes toutes différentes. A chaque tour, je pioche une carte, je note sa valeur, puis la remets dans le paquet, je mélange et recommence.
Combien de fois dois-je piocher des cartes pour être sûr (à 95% de chance) d'avoir eu au moins 5 cartes différentes au cours de mes pioches ?

Bonne journée, et merci d'avance,

Alex

[Ben314]

Salut
Ce genre de truc, ça peut se faire très simplement avec un tableur.
Tu prévois 6 colonnes :
A = Numéro du tirage ;
B =Proba. d'avoir tiré toujours la même carte ;
C =proba de n'avoir tiré exactement 2 cartes différentes ;
D =proba de n'avoir tiré exactement 3 cartes différentes ;
E =proba de n'avoir tiré exactement 4 cartes différentes ;
F =proba de n'avoir tiré au moins 5 cartes différentes ;
que tu initialise (1ère ligne) avec 1 ; 1 ; 0 ; 0 ; 0 ; 0 puis sur la deuxième ligne tu rentre les formules (évidente)
;
;
;
;
;

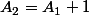et tu n'a plus qu'à recopier cette deuxième ligne autant de fois que nécessaire pour avoir tout les résutat que tu veut.

[Alex060496]

Tout d'abord merci pour la réponse. Cette solution fonctionne effectivement sur le problème simplifié que j'ai énoncé, j'ai cependant mal évalué les limites de mon énoncé ^^'. Les choses se compliquent quand je passe à mon réel problème :
Je tente de cartographier l'ensemble du génome d'un organisme par des insertions aléatoires de petites séquences. L'outil que j'utilise est bâti de tel sorte que j'ai théoriquement 396 172 sites d'insertion potentiel sur l'ensemble du génome (pas un de plus, pas un de moins ^^). Il n'est ni réaliste, ni nécessaire que j'obtienne un mutant représentatif de chacun de ces 390 000+ sites, cependant je voudrais utiliser les probabilités afin d'estimer le nombre de mutants que je vais devoir générer afin d'en couvrir une certaine proportion.

Mon problème devient donc :
J'ai 396 172 sites différents. A chaque nouveau mutant indépendant généré, j'aurai obtenu au hasard un site parmi ces 396 172 sites.
Combien de mutants indépendants dois-je générer si je veux être quasi sûr (95%) d'avoir obtenu au moins un exemple de 50% de tous les sites potentiels (donc au moins 198086 sites différents) ?

Merci d'avance,
Alex

[mathelot]

Combien de fois dois-je piocher des cartes pour être sûr (à 95% de chance) d'avoir eu au moins 5 cartes différentes au cours de mes pioches ?

On a un paquet de 10 cartes distinctes.
on pioche 1 carte, par exemple

puis après on peut tirer fois la même carte
puis on tire ensuite une deuxième carte
puis après on peut tirer fois les mêmes cartes ou
puis on tire ensuite une troisième carte
puis après on peut tirer fois les mêmes cartes ou ou
etc..

La proba de tirer cinq cartes distinctes est:



La somme se simplifie en:


La somme se minore par:


on pose

il suffit que


ce qui donne

Un nombre de tirages suffisant pour tirer 5 cartes distinctes avec remise , avec une proba supérieure à 0,95 est donc

[Ben314]

Vu la taille du 396 172, ça doit être encore jouable de faire un calcul du style "tableur" ci dessus, mais ça demande un outil plus performant qu'un tableur et une assez bonne maîtrise de l'outil pour être sûr que le cumul des erreurs faites à chaque calcul ne rend pas le résultat caduc.

Sinon, on peut faire une estimation. Vu le contexte je pense que ça doit être suffisant.
Si on tire au hasard (avec remise) M "objets" parmi N et qu'on intéresse au nombre d'objets différents tirés, on peut écrire que où vaut 1 ou 0 selon que l'objet numéro a été tiré (au moins une fois) ou pas.
La loi des est évidente : et, bien que les différents ne soient pas indépendants, l'espérance de leur somme est égale à la somme des espérances : avec (pour "grand").
Avec le même type de calculs en légèrement plus complexes, on peut calculer puis la variance :

(calculs à vérifier vu que j'ai fait ça vite fait et... à la main...)

Avec ça et, soit en considérant que la loi est plus ou moins une gaussienne, soit en utilisant l'inégalité de Bienaymé-Tchebychev, tu doit pouvoir trouver pour quel M tu aura au moins 95% de chance que X soit supérieur ou égal à une barre donnée (je pourrais te faire les calculs jusqu'au bout, mais là, j'ai absolument rien sous la main pour le faire donc j'espère que quelqu'un d'autre vérifiera la variance et finira le calcul. . .)

[LB2]

Hello,

je pense que le logiciel R est un meilleur outil que le tableur pour ton problème. Voici quelques ressources qui pourront t'aider :

https://rafalab.github.io/pages/harvardx.html
https://compgenomr.github.io/book/

[Ben314]

Si N=396 172 et M=276 172 l'espérance de X est 198 867,7 et sa variance 30 542,3.
L'inégalité de Bienaymé-Tchebychev dit alors que la proba. que X <198086=N/2 est inférieure à 4,998%.
En fait, pour un N quelconque (grand), pour que l'approximation de E(X) soit égale à N/2, il faut prendre c'est à dire (=274 606 si N=396 172) et, vu que la variance est très faible relativement à l'espérance il suffit de prendre "un peu plus" pour garantir à 95% que X est >N/2.

[tournesol]

bonsoir à tous
pour le pb des cartes j'ai trouvé 9 tirages pour garantir 0,958% , et ce avec une formule sommatoire exacte que je n'ai pas le temps d'expliciter maintenan(télé oblige)

[GaBuZoMeu]

La méthode proposée par Ben était aussi exacte : elle consiste à calculer



et à constater le premier pour lequel la dernière coordonnée du vecteur obtenu est supérieure ou égale à 0,95

Code: Tout sélectionner

M=matrix(QQ,5,5)
for i in range(4) : M[i,0]=(i+1)/10 ; M[i,i+1]=(9-i)/10
M[4,4]=1
V=vector(QQ,5)
V[0]=1
for n in range(23,28) :
    print("probabilité d'avoir au moins 5 cartes différentes en",n,"tirages :")
    proba=(V*M^(n-1))[-1]
    print(proba, "soit environ", (100*proba).n(13),"%")

donne :

probabilité d'avoir au moins 5 cartes différentes en 23 tirages :
577096980431223837501/625000000000000000000 soit environ 92.3 %
probabilité d'avoir au moins 5 cartes différentes en 24 tirages :
5828564800214477490267/6250000000000000000000 soit environ 93.2 %
probabilité d'avoir au moins 5 cartes différentes en 25 tirages :
11758366523938873807017/12500000000000000000000 soit environ 94.1 %
probabilité d'avoir au moins 5 cartes différentes en 26 tirages :
592377540636238049411019/625000000000000000000000 soit environ 94.8 %
probabilité d'avoir au moins 5 cartes différentes en 27 tirages :
5963028037186411086342237/6250000000000000000000000 soit environ 95.4 %

Sage Math trouve 27 tirages. Qui a raison ?

Ce genre de truc avec une matrice de taille environ 200 000, ça devient problématique !

[tournesol]

je vais donner ma methode mais au vu de ce que vous trouvez , elle risque d'être erronée .
un tirage de n cartes est une application T de [1,n] dans [1;10]
Il y a 10^n telles applications .
Le tirage T contient au moins 5 cartes différentes ssi card(im(T))5
soit donc k compris entre 5 et 10 .
un tirage T dont le cardinal de l'image est égal à k est déterminé par le choix de im(T) ( possibilités) , puis par une surjection de [1,n] sur im(T) . Si je note s(n,k) le nombre de ces surjections , alors le nombres de tirages favorables est égal à
en divisant ce nombre par 10^n , on obtient la probabilité .
n=5 donne 0,3024 n=6 donne 0,6048 n=7 donne 0,80136 n=8 donne 0,9072 n=9 donne 0,95863824

[Ben314]

Il me semble bien que les 2/10 ; 3/10 et 4/10 ne sont pas placés au bon endroit. Ils devraient être sur la diagonale principale et pas dans la première colonne vu que c'est les cas où on ne tire pas de nouvelle carte (donc le nombre de carte tirée reste constant alors qu'avec ta matrice il redescend à 1)

Même problème dans le programme en python lors de l'initialisation de M où ça devrait être M|i,i]=(i+1)/10 et pas M[i,0]=(i+1)/10.

[tournesol]

Pour 2a sites , la formule devient

[tournesol]

les inégalités de Bernstein sont plus performantes que celle de Bienaymé Tchebychev.

[GaBuZoMeu]

Au temps pour moi, tu as raison Ben ! La bonne matrice est effectivement



le bon code est

Code: Tout sélectionner

M=matrix(QQ,5,5)
for i in range(4) : M[i,i]=(i+1)/10 ; M[i,i+1]=(9-i)/10
M[4,4]=1
V=vector(QQ,5)
V[0]=1
for n in range(6,10) :
    print("probabilité d'avoir au moins 5 cartes différentes en",n,"tirages :")
    proba=(V*M^(n-1))[-1]
    print(proba, "soit environ", (100*proba).n(13),"%")

probabilité d'avoir au moins 5 cartes différentes en 6 tirages :
378/625 soit environ 60.5 %
probabilité d'avoir au moins 5 cartes différentes en 7 tirages :
10017/12500 soit environ 80.1 %
probabilité d'avoir au moins 5 cartes différentes en 8 tirages :
567/625 soit environ 90.7 %
probabilité d'avoir au moins 5 cartes différentes en 9 tirages :
5991489/6250000 soit environ 95.9 %

Tournesol avait raison, SageMath avait raison mais c'est juste moi qui m'étais trompé !

[tournesol]

Merci GaBuZoMeu . Casio graph 35 + vient de me donner 956 tirages favorables pour 1000 tirages simulés .