Probabilité de k faces consécutifs sur N lancers P/F
24 messages
- Page 1 sur 2 - 1, 2
Probabilité de k faces consécutifs sur N lancers P/F
Bonjour,
J’ai une question de probabilité qui n’est pas trop compliquée à comprendre, mais qui me pose problème. J’ai cherché à l’aborder de plusieurs manières, mais en vain. Voici le problème :
On considère N lancers identiques et indépendants de pile ou face (ou autre jeu, tant qu’il n’y a que 2 issues) avec une probabilité P d’obtenir pile.
Quel est la probabilité d’obtenir une fois exactement k face consécutifs sur les N lancers ?
Quel est la probabilité d’obtenir une fois plus de k face consécutifs sur les N lancers ?
Par exemple, on fait N=100 lancers. Quel est la proba d’avoir disons 5 piles puis k=25 faces puis apres des piles OU des faces mais jamais plus de 25 faces de suites sur les lancers restants.
J’ai tenté par des dénombrements et autres, mais je n’ai pas trouvé la formule. C’est ce que je cherche ; une formule qui donne cette proba en fonction de N, k, et p..
Merci d’avance pour votre aide,
Bonne journée
J’ai une question de probabilité qui n’est pas trop compliquée à comprendre, mais qui me pose problème. J’ai cherché à l’aborder de plusieurs manières, mais en vain. Voici le problème :
On considère N lancers identiques et indépendants de pile ou face (ou autre jeu, tant qu’il n’y a que 2 issues) avec une probabilité P d’obtenir pile.
Quel est la probabilité d’obtenir une fois exactement k face consécutifs sur les N lancers ?
Quel est la probabilité d’obtenir une fois plus de k face consécutifs sur les N lancers ?
Par exemple, on fait N=100 lancers. Quel est la proba d’avoir disons 5 piles puis k=25 faces puis apres des piles OU des faces mais jamais plus de 25 faces de suites sur les lancers restants.
J’ai tenté par des dénombrements et autres, mais je n’ai pas trouvé la formule. C’est ce que je cherche ; une formule qui donne cette proba en fonction de N, k, et p..
Merci d’avance pour votre aide,
Bonne journée
Re: Probabilité de k faces consécutifs sur N lancers P/F
Bonjour,
un seul lancer de Pile ou Face, c'est une épreuve de Bernoulli,
l'une des deux issues s'appelle Succès, et l'autre Échec.
Plusieurs épreuves de Bernoulli, identiques, successives et indépendantes,
dont on veut savoir le nombre de succès, c'est la loi binomiale, (c'est dans ton cours).
Cordialement,
--
Mateo.
un seul lancer de Pile ou Face, c'est une épreuve de Bernoulli,
l'une des deux issues s'appelle Succès, et l'autre Échec.
Plusieurs épreuves de Bernoulli, identiques, successives et indépendantes,
dont on veut savoir le nombre de succès, c'est la loi binomiale, (c'est dans ton cours).
Cordialement,
--
Mateo.
Re: Probabilité de k faces consécutifs sur N lancers P/F
Bonjour,
Je ne comprends pas très bien le sens de cette question :
Peux-tu préciser ?
À vrai dire, je ne comprends pas très bien le sens de la première non plus.
Si on fait une fois 25 faces de suite exactement et plus tard 30 faces de suite exactement, on a bien fait "une fois exactement 25 faces consécutifs" ou pas ?
Je ne comprends pas très bien le sens de cette question :
Quel est la probabilité d’obtenir une fois plus de k face consécutifs sur les N lancers ?
Peux-tu préciser ?
À vrai dire, je ne comprends pas très bien le sens de la première non plus.
Si on fait une fois 25 faces de suite exactement et plus tard 30 faces de suite exactement, on a bien fait "une fois exactement 25 faces consécutifs" ou pas ?
Re: Probabilité de k faces consécutifs sur N lancers P/F
Effectivement, je n'ai pas été bien clair... je reformule.
On fait 100 lancers de pile ou face. Je cherche la probabilité qu'il y est par exemple 25 faces à la suite, en sachant qu'il n'y a pas de plus gros bloc consécutifs avant, mais peu importe ce qu'il y a après (il peut y en avoir très bien 6 consécutifs après ou même 40 ce n'est pas grave).
On fait 100 lancers de pile ou face. Je cherche la probabilité qu'il y est par exemple 25 faces à la suite, en sachant qu'il n'y a pas de plus gros bloc consécutifs avant, mais peu importe ce qu'il y a après (il peut y en avoir très bien 6 consécutifs après ou même 40 ce n'est pas grave).
Re: Probabilité de k faces consécutifs sur N lancers P/F
Mateo_13 a écrit:Bonjour,
un seul lancer de Pile ou Face, c'est une épreuve de Bernoulli,
l'une des deux issues s'appelle Succès, et l'autre Échec.
Plusieurs épreuves de Bernoulli, identiques, successives et indépendantes,
dont on veut savoir le nombre de succès, c'est la loi binomiale, (c'est dans ton cours).
Cordialement,
--
Mateo.
La loi binomiale te donne le nombre de succès sur N lancers. Mais elle ne te donne pas L'ORDRE dans lequel les succès sont apparues et donc tu n'as pas accès à leur position( c'est d'ailleurs pour ça qu'il y a le coefficient binomial dans la formule pour calculer la proba). Ici dans mon problème il y a des positions à respecter. Il y a plein de configurations qui amènent à 25 succès sur 100 lancers par exemple. C'est précisément cela que je n'arrive pas à dénombrer sous les conditions du problèmes (k faces consécutifs sur N lancers, sans avoir plus avant que les k faces arrivent, et peu importe ce qu'il y a après).
Cordialement
Re: Probabilité de k faces consécutifs sur N lancers P/F
Salut,
Si je comprend bien, ce que tu cherche, c'est la loi de la variable aléatoire X qui donne la longueur de la plus grande série de piles consécutifs obtenue lors d'une série de N lancés de pile/face (avec proba de pile = p pas forcément égal à 1/2).
Si je comprend bien, ce que tu cherche, c'est la loi de la variable aléatoire X qui donne la longueur de la plus grande série de piles consécutifs obtenue lors d'une série de N lancés de pile/face (avec proba de pile = p pas forcément égal à 1/2).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Probabilité de k faces consécutifs sur N lancers P/F
Est ce bien les probabilités de ces deux évènements que tu veux calculer ?
Obtenir au moins 25 piles consécutifs .
La plus grande suite de piles consécutifs est de longueur 25 .
Obtenir au moins 25 piles consécutifs .
La plus grande suite de piles consécutifs est de longueur 25 .
Re: Probabilité de k faces consécutifs sur N lancers P/F
Je ne sais pas si j'ai bien compris.
événement A0 : tirages ayant k faces consécutifs commençant au début.
événement Ai pour i allant de 1 à N-k : tirages ayant un pile en n°i suivi de k faces consécutifs.
Tu veux calculer la probabilité de la réunion des Ai pour i de 0 à N-k. C'est ça ?
On calcule par principe d'inclusion-exclusion. C'est pénible, mais ça se fait (et ça se programme).
Il y a peut-être moins bourrin.
événement A0 : tirages ayant k faces consécutifs commençant au début.
événement Ai pour i allant de 1 à N-k : tirages ayant un pile en n°i suivi de k faces consécutifs.
Tu veux calculer la probabilité de la réunion des Ai pour i de 0 à N-k. C'est ça ?
On calcule par principe d'inclusion-exclusion. C'est pénible, mais ça se fait (et ça se programme).
Il y a peut-être moins bourrin.
Re: Probabilité de k faces consécutifs sur N lancers P/F
Ben314 a écrit:Salut,
Si je comprend bien, ce que tu cherche, c'est la loi de la variable aléatoire X qui donne la longueur de la plus grande série de piles consécutifs obtenue lors d'une série de N lancés de pile/face (avec proba de pile = p pas forcément égal à 1/2).
Pas forcément de la plus grande, mais la probabilité qu'une série dépasse un seuil, oui. Par exemple la proba qu'il y est au moins une série d'au moins k faces de suite pour commencer simplement. Puis dans l'idéal avoir la proba qu'il y est au moins une série d'exactement k faces de suite.
Mais, avoir un résultat "pour au moins k faces consécutifs", ça serait déjà le top..
Re: Probabilité de k faces consécutifs sur N lancers P/F
tournesol a écrit:Est ce bien les probabilités de ces deux évènements que tu veux calculer ?
Obtenir au moins 25 piles consécutifs .
La plus grande suite de piles consécutifs est de longueur 25 .
Oui : "obtenir au moins une série d'au moins k (par exemple k=25) piles (ou face après tout on peut simplement changer p en 1-p) consécutifs sur N (par exemple N=100) lancers.
Re: Probabilité de k faces consécutifs sur N lancers P/F
GaBuZoMeu a écrit:Je ne sais pas si j'ai bien compris.
événement A0 : tirages ayant k faces consécutifs commençant au début.
événement Ai pour i allant de 1 à N-k : tirages ayant un pile en n°i suivi de k faces consécutifs.
Tu veux calculer la probabilité de la réunion des Ai pour i de 0 à N-k. C'est ça ?
On calcule par principe d'inclusion-exclusion. C'est pénible, mais ça se fait (et ça se programme).
Il y a peut-être moins bourrin.
Oui, je crois bien que c'est ça, si je t'ai bien compris. Dans le sens où la réunion des Ai représenterait les tirages avec une série d'au moins k faces à la suite. D'ailleurs, si je comprends bien, cela permettra de compter les tirages avec une unique série de k faces c'est bien ça ? Dans tout les cas c'est déjà super !
Par contre, je ne vois pas la façon dont tu le calculerais, par inclusion exclusion. Je n'ai pas ou peu fais ce genre de calculs, notamment dans ce contexte..
Re: Probabilité de k faces consécutifs sur N lancers P/F
cela permettra de compter les tirages avec une unique série de k faces c'est bien ça ?
Non. avec au moins une suite de k faces consécutives. C'est justement pour ça que l'intersection des Ai n'est pas vide, et qu'il faut compter par inclusion exclusion pour ne pas faire de compte multiple.
Inclusion-exclusion, ça veut dire qu'on fait la somme des probabilités des Ai, qu'on retire la somme des probabilités des intersections 2 à 2, qu'on ajoute la somme des probabilités des intersections 3 à 3 etc.
Pour N=100 et k=25, les intersections 4 à 4 sont vides, alors on s'arrête là.
Re: Probabilité de k faces consécutifs sur N lancers P/F
GaBuZoMeu a écrit:cela permettra de compter les tirages avec une unique série de k faces c'est bien ça ?
Inclusion-exclusion, ça veut dire qu'on fait la somme des probabilités des Ai, qu'on retire la somme des probabilités des intersections 2 à 2, qu'on ajoute la somme des probabilités des intersections 3 à 3 etc.
Pour N=100 et k=25, les intersections 4 à 4 sont vides, alors on s'arrête là.
AH oui oui je vois ! Effectivement c'est laborieux... surtout si N devient grand. En pratique je comptais appliquer tout ça pour des valeurs de N de l'ordre plusieurs milliers voir dizaine de milliers. Et chercher k tel que la proba qu'on trouve une série supérieur à k soit inférieur à un seuil prédéfini.
J'ai pu programmer quelques simulations, mais les nombres ne sont pas parfaitement aléatoires et je ne suis pas spécialisé en info, donc mes résultats de simulations portent forcément des erreurs... Alors c'est pour cela que je cherche une formule explicite entre cette proba et k (dans l'idéal non récurrente..). Si d'autres idées te viennent n'hésite pas à me les partager je suis tout ouïe, merci déjà pour ton aide !
Re: Probabilité de k faces consécutifs sur N lancers P/F
Formule explicite, je ne vois pas trop.
Mais un petit programme python pour calculer ça, même pour des grands N, ça me semble loin d'être insurmontable ! Tu ne veux pas essayer ?
Mais un petit programme python pour calculer ça, même pour des grands N, ça me semble loin d'être insurmontable ! Tu ne veux pas essayer ?
Re: Probabilité de k faces consécutifs sur N lancers P/F
Celui qui propose une simulation va peut être sauver le soldat Bryan...
-->[]
-->[]
la vie est une fête 
Re: Probabilité de k faces consécutifs sur N lancers P/F
Bonjour,
un lien vers un article un peu technique sur la loi de la variable aléatoire égale à la longueur de la plus longue série de Piles dans un Pile ou Face (équilibré ou non) de longueur n : https://alexamarioarei.github.io/Resear ... Review.pdf.
Son espérance vaut à peu près+\gamma}{ln(2)} - \frac{3}{2}) où
où  est la constante d'Euler. Ce qui est intéressant, c'est que la variance de cette variable aléatoire est assez faible (Pour n grand, son écart type est environ 1.873).
est la constante d'Euler. Ce qui est intéressant, c'est que la variance de cette variable aléatoire est assez faible (Pour n grand, son écart type est environ 1.873).
A vérifier avec des simulations Python!
un lien vers un article un peu technique sur la loi de la variable aléatoire égale à la longueur de la plus longue série de Piles dans un Pile ou Face (équilibré ou non) de longueur n : https://alexamarioarei.github.io/Resear ... Review.pdf.
Son espérance vaut à peu près
A vérifier avec des simulations Python!
Modifié en dernier par LB2 le 19 Mai 2020, 11:37, modifié 2 fois.
Re: Probabilité de k faces consécutifs sur N lancers P/F
Ah, en fait il y a plus simple que ce que je proposais : je n'ai pas assez le réflexe markovien !
Donc une chaîne de Markov avec états
états 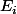 pour
pour  de
de  à
à 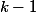 : les
: les  derniers tirages sont des faces (et pas les
derniers tirages sont des faces (et pas les 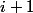 derniers), plus l'état final (absorbant)
derniers), plus l'état final (absorbant) 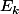 = bingo ! Quand on arrive à
= bingo ! Quand on arrive à 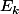 , on y reste ; la probabilité de passer de
, on y reste ; la probabilité de passer de 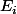 à
à 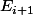 est
est  , sinon on revient à
, sinon on revient à 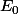 .
.
Il suffit d'avoir la puissance -ème de la matrice de transition, appliqué à la distribution initiale : tout sur
-ème de la matrice de transition, appliqué à la distribution initiale : tout sur 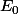 .
.
Donc une chaîne de Markov avec
Il suffit d'avoir la puissance
Re: Probabilité de k faces consécutifs sur N lancers P/F
Cette question est connue sous le terme 'The longest run'.
C'est d'ailleurs le titre de l'article donné par LB2.
En cherchant cette expression, tu devrais trouver plein de trucs sur le sujet.
C'est d'ailleurs le titre de l'article donné par LB2.
En cherchant cette expression, tu devrais trouver plein de trucs sur le sujet.
Re: Probabilité de k faces consécutifs sur N lancers P/F
Bon, avec les techniques habituelles de chaînes de Markov avec état absorbant, un petit code écrit en Sagemath :
et puis on l'utilise pour voir la probabilité d'obtenir au moins k faces de suites en N tirages, pour une pièce équilibrée :

- Code: Tout sélectionner
def Probsuite(N,k,p) :
Q=matrix(RR,k,k)
for i in range(k) : Q[i,0]=1-p
for i in range(k-1) : Q[i,i+1]=p
R=vector(RR,k)
R[k-1]=p
I=identity_matrix(k)
S=(I-Q)**(-1)*(I-Q**N)*R
return S[0]
et puis on l'utilise pour voir la probabilité d'obtenir au moins k faces de suites en N tirages, pour une pièce équilibrée :
- Code: Tout sélectionner
Liste=[(k,Probsuite(10000,k,.5)) for k in range(10,25)]
Listebis=[(k,Probsuite(100000,k,.5)) for k in range(10,25)]
l=line(Liste,marker="o")
t=text("N = 10000",(11.5,.4))
lbis=line(Listebis,marker="o",color="red")
tbis=text("N = 100000",(17.5,.6),color="red")
show(l+lbis+t+tbis)

Re: Probabilité de k faces consécutifs sur N lancers P/F
LB2 a écrit:Bonjour,
un lien vers un article un peu technique sur la loi de la variable aléatoire égale à la longueur de la plus longue série de Piles dans un Pile ou Face (équilibré ou non) de longueur n : https://alexamarioarei.github.io/Resear ... Review.pdf.
Son espérance vaut à peu prèsoù
est la constante d'Euler. Ce qui est intéressant, c'est que la variance de cette variable aléatoire est assez faible (Pour n grand, son écart type est environ 1.873).
A vérifier avec des simulations Python!
Merci beaucoup je vais regarder ça de plus près !!
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
