Je crois que tout est dans le titre, plus précisement je chercher à explicité le terme P(X=i) dans la fonction génératrice ( ici i est compris entre k et 6k pour k lancés).
Par exemple pour 5 lancers, determiner la probabilité d'obtenir 14 ( en faisant la somme des des 5 dés ). Le dénominateur étant connu ( 6^5 ) j'aimerais un petit coup de main.
Merci ;)
Proba: Somme de n lancers de dés
6 messages
- Page 1 sur 1
par alavacommejetepousse » 11 Fév 2010, 12:17
bonjour
il n y a pas de formule très simple
c'est celle qui donne les coefficients du produit de polynômes
il faut compter les k listes d'entiers compris entre 0 et 6 de somme égale à i
l'absence de formule exploitable vient de la tronquature à 6
as -tu déjà la formule pour 2 dés ?
il n y a pas de formule très simple
c'est celle qui donne les coefficients du produit de polynômes
il faut compter les k listes d'entiers compris entre 0 et 6 de somme égale à i
l'absence de formule exploitable vient de la tronquature à 6
as -tu déjà la formule pour 2 dés ?
par Ineedi2 » 12 Fév 2010, 11:30
Rebonjour,
désolé pour la réponse tardive, mais je serai devant le pc jusqu'à 16h si certains veulent bien me donner un coup de main. Pour répondre à ta question je vais avant tout voir comment on code les symboles ici sinon je vais te donner un truc affreux.
A tout de suite
désolé pour la réponse tardive, mais je serai devant le pc jusqu'à 16h si certains veulent bien me donner un coup de main. Pour répondre à ta question je vais avant tout voir comment on code les symboles ici sinon je vais te donner un truc affreux.
A tout de suite
par Ineedi2 » 12 Fév 2010, 11:48
Alors voici ce que je trouve pour deux lancés:
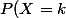 = \bigsum_{i=0}^{12} P(X=i) * P(X=k-i))
Bien sur je prends en compte ici que P(X=k) = 0 Pour k différent de {1,2,3,4,5,6}.
Alors généraliser cette formule rien que pour 3 lancées me pose déjà un soucis, je me demande si je devrais pas plutot chercher une formule me donnant les coefficients des t pour^n)
.
Qu'en pensez vous ?
Bien sur je prends en compte ici que P(X=k) = 0 Pour k différent de {1,2,3,4,5,6}.
Alors généraliser cette formule rien que pour 3 lancées me pose déjà un soucis, je me demande si je devrais pas plutot chercher une formule me donnant les coefficients des t pour
Qu'en pensez vous ?
par Ineedi2 » 12 Fév 2010, 13:57
Bon en fait l'énoncé nous donne la réponse à trouver, je pose le problème pour etre le plus clair possible:
On lance n fois de suite un dé normal. Soit
la va égale au chiffre obtenu pour un lancer de dé ; soit la variable aléatoire égale au chiffe obtenu au i-ème lancer et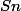 
la va égale à la somme des chiffres obtenus.
Pour k>=n, montrez que :
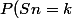 = \frac{1}{6^n} \bigsum_{i=0}^{min(n,\frac{(k-n)}{6})} (-1)^i \begin{pmatrix}<br />n \\<br />i<br />\end{matrix} \begin{pmatrix}<br />k-6&-1 \\<br />n-1<br />\end{matrix})
Alors si vous avez une piste, je suis tout ouie.
Merci à bientot
On lance n fois de suite un dé normal. Soit
Pour k>=n, montrez que :
Alors si vous avez une piste, je suis tout ouie.
Merci à bientot
par ffpower » 12 Fév 2010, 18:53
A mon avis l idée du polynome est bonne. J ai la flemme de faire les calculs mais
on peut par exemple ecrire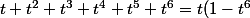/(1-t))
donc^n=t^n(1-t^6)^n/(1-t)^n)
.
-Les coeff de (1-t^6)^n se calculent par le binome.
-^n)
, c est la dérivée (n-1)-ieme de =1+t+t^2+...)
. Donc ses coeffs ce calculs aussi.
-On peut alors calculer les coeffs de^n/(1-t)^n)
en faisant un produit de Cauchy
-On multiplie le tout par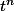
, et on a fini.
on peut par exemple ecrire
donc
-Les coeff de (1-t^6)^n se calculent par le binome.
-
-On peut alors calculer les coeffs de
-On multiplie le tout par
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :