[Analyse complexe] Principe du maximum

[Alekeus]

Bonjour à tous,

Etant donné que je suis nouveau sur le forum, je me permets de me présenter très vite. Je m'appelle Alex, 21 ans, initialement de formation STI en génie mécanique j'ai intégré il y a deux ans une école d'ingénieurs en aéronautique post-bac. Je suis donc aujourd'hui en année bac+3 et ressortissant STI je prends toujours un peu plus de temps que les autres pour comprendre les maths.

Je bloque ici sur un travail que le professeur nous a donné en analyse complexe, à savoir faire la démonstration du principe du maximum, que l'on a sous cette forme :

Si une fonction holomorphe dans n'est pas constante, alors elle atteint son maximum (en module) sur sa frontière

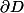
Il nous a conseillé d'utiliser toutes les hypothèses simplificatrices et de faire la démo par l'absurde. Seulement, j'ai du mal à appréhender la question. En général lorsqu'un problème se pose, je vois déjà à peu près les étapes se construire dans ma tête mais là c'est le vide total pour moi, un vrai charabia.

Après recherches j'ai bien sûr trouvé des tas de démonstrations mais pareil, je ne vois pas la logique et je trouve absurde de rendre un travail que je ne comprend pas moi-même. Je vous appelle donc à l'aide, pour quelques explications si possible un peu plus concrètes de ce théorème. Je pense aussi que mes lacunes avec les ensembles (ouvert, fermé, connexe) en ajoutent à mon incompréhension, donc si quelqu'un a de quoi clarifier les choses je pense qu'en partant de là tout irait mieux.

Je signale aussi en passant que ce travail est facultatif, pas obligé de le rendre, c'est seulement un moyen d'obtenir des points en plus et surtout mieux comprendre le cours.

Je vous remercie d'avance et vous souhaite une agréable journée !

Alekeus

[arnaud32]

de quels resultats sur les fonctions holomorphes disposes tu?

[Alekeus]

Alors jusque là on a vu le Théorème de Cauchy dans un domaine simplement connexe (l'intégrale ne dépend pas du chemin) et sa corollaire, des propriétés similaires à celles des intégrales réelles, le théorème de Morera, puis on a généralisé au cas multiplement connexe. Ensuite, on a vu la formule de cauchy avec C un chemin contenu dans D et tournant une fois autour de z dans le sens trigo. Enfin, la formule de la moyenne et on en est restés au principe du maximum.

Avant tout ça, c'était des choses assez simples, des propriétés d'intégrales et un passage de topologie sur la connexité mais que je n'ai pas vraiment compris... J'espère avoir répondu à la question ? Sinon je peux poster directement mon cours en format pdf si c'est plus simple ?

[arnaud32]

as tu vu le fait qu'une fonction holomorphe est analytique?

[Alekeus]

Oui on l'a vu dans le chapitre précédent ! On a simplement dit qu'une fonction analytique admet localement un développement en série de puissances entières positives.

[arnaud32]

tu suppose que le maximum est atteint en z_0 a l'interrieur de D
tu as alors au voisinage de z_0
avec p>0

tu vas essayer de bien choisir pour trouver une contradiction

en particulier le choix de t est important
tu peux utiliser |u+v|>| |u|-|v| |

[Alekeus]

D'accord je vais m'y mettre dans la soirée alors ! Merci beaucoup ! Je pourrais poster ce que j'aurai fait pour avoir une petite correction au cas où il y aurait des inexactitudes ?

[arnaud32]

D'accord je vais m'y mettre dans la soirée alors ! Merci beaucoup ! Je pourrais poster ce que j'aurai fait pour avoir une petite correction au cas où il y aurait des inexactitudes ?

oui avec ca t'es sur la bonne voie

[Alekeus]

Bonsoir,

Quelque chose me turlupine encore, j'espère que je ne suis pas trop embêtant... Alors après encore quelques recherches je me demande finalement si la méthode que tu me propose convient bien. En effet, par rapport au fait que f est analytique, nous n'avons vu qu'une ligne qui en parle vaguement dans le chapitre précédent et je ne crois pas que ce soit ce que le prof recherche en vérité. J'ai peur qu'il me demande d'où je sors mes formules sans pouvoir lui expliquer clairement...

Dans le cours, juste avant le principe du max, nous voyons la formule de la moyenne :

Et je remarque qu'il y a la forme du z+r*exp(it) dans cette formule. Est-il possible d'en faire quelque chose dans ma démo, de manière à assurer une certaine continuité avec le cours ?

[Doraki]

si |f| est atteint en z à l'intérieur du domaine,
alors pour r suffisemment petit pour que f(z+re^2i;)t) soit encore dans D pour tout t,
|f(z)| = |intégrale sur [0;1] de f(z+re^2i;)t)| <= intégrale sur [0;1] de |f(z+re^2i;)t)| <= intégrale sur [0;1] de |f(z)| = |f(z)|
Donc les deux inégalités sont en fait des égalités.
Non seulement |f(z+re^2i;)t)| = |f(z)| tout autour de z, mais en plus l'inégalité de la moyenne est une égalité donc les trucs à l'intérieur de l'intégrale ont tous le même argument, donc f est constante autour de z.
Et donc elle est constante sur D (pourvu qu'il soit connexe)

[Alekeus]

Okay je vois le raisonnement maintenant merci pour ta réponse!

Par contre pour poser |f(z)| = |intégrale sur [0;1] de f(z+re^2i;)t)| est ce que tu fais un changement de variable? Parce que je ne vois pas lequel du coup.

EDIT: Plus précisément, je ne vois pas pourquoi l'intégrale va de 0 à 1, pour le reste ca va en fait x)

[Doraki]

ouais j'avais la flemme de tout diviser par 2;) alors j'ai remplacé t par 2;)t.

[Alekeus]

ouais j'avais la flemme de tout diviser par 2;) alors j'ai remplacé t par 2;)t.

D'accord je vois maintenant, merci pour tout et bonne soirée !!

[Alekeus]

Désolé mais en fait j'ai encore du mal à me représenter les choses. Graphiquement ca donnerait quoi par exemple? Je ne vois pas trop le rapport entre le fait que le fonction soit continue et qu'elle atteigne son max à la frontière du domaine connexe ou pas, je crois que je m'embrouille depuis le début...

[Doraki]

Graphiquement, si t'as une fonction holomorphe non constante définie autour d'un point z, |f| ne peut pas avoir de maximum local en z. Il y aura toujours des directions où tu peux bouger z pour faire augmenter |f(z)|.

Si D est un ouvert borné de C, et que tu essayes de suivre un chemin qui fait augmenter |f| indéfiniment tu vas forcément arriver à la frontière de D au bout d'un moment et tu ne pourras plus continuer. Donc tu tombes sur un maximal local de |f| à la frontière de D.