Principe du maximum
15 messages
- Page 1 sur 1
Principe du maximum
Bonjour,
Est-ce que quelqu'un pourrait me dire, ce que signifie (une interprétation physique, ou géométrique), en général (ou me donner un lien).
En effet, j'ai rencontré cette expression dans plusieurs champ des mathématiques, sans véritablement avoir pris la mesure de l'expression.
Je connais les preuves mathématiques, mais si on me demande ce que c'est que le principe du maximum je suis incappable de répondre...
Merci
Est-ce que quelqu'un pourrait me dire, ce que signifie (une interprétation physique, ou géométrique), en général (ou me donner un lien).
En effet, j'ai rencontré cette expression dans plusieurs champ des mathématiques, sans véritablement avoir pris la mesure de l'expression.
Je connais les preuves mathématiques, mais si on me demande ce que c'est que le principe du maximum je suis incappable de répondre...
Merci
Le principe du maximum est un résultat sur les fonctions analytiques complexes. Dans sa formulation la plus générale, c'est à dire pour plusieurs variables, ce résultat est le suivant:
Soit P un polydisque ouvert contenant l'origine dans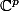 et
et 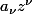 une série entière à p variables complexes (
une série entière à p variables complexes (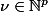 ) et à coefficients dans un espace de Banach complexe E. Soit
) et à coefficients dans un espace de Banach complexe E. Soit  sa somme.
sa somme.
S'il existe une boule ouverte autour de l'origine 0 de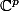 telle que, pour tout
telle que, pour tout 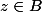 , on a
, on a | < |f(0)|) alors f est constante.
alors f est constante.
Cette propriété n'est pas vraie pour les fonctions analytiques réelles comme le montre l'exemple de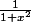 .
.
Une conséquence de ce thèorème est que, pour une fonction analytique complexe définie sur un ouvert A, les points où elle atteint son maximum sur un compact K inclus dans A sont situés sur la frontière de K.
Quand on étudie attentivement la démonstration de ce théorème, on s'aperçoit qu'elle met en évidence une propriété surprenante de la variable complexe: l'existence d'un continuum de valeurs pour l'argument (au lieu des seules possibilités +1 et -1 dans le cas réel), associée au type spécial de "relation" locale entre points voisins imposée par la dérivabilité complexe, obligent une "rigidisation" du graphe de la fonction dans le cas complexe.
Soit P un polydisque ouvert contenant l'origine dans
S'il existe une boule ouverte autour de l'origine 0 de
Cette propriété n'est pas vraie pour les fonctions analytiques réelles comme le montre l'exemple de
Une conséquence de ce thèorème est que, pour une fonction analytique complexe définie sur un ouvert A, les points où elle atteint son maximum sur un compact K inclus dans A sont situés sur la frontière de K.
Quand on étudie attentivement la démonstration de ce théorème, on s'aperçoit qu'elle met en évidence une propriété surprenante de la variable complexe: l'existence d'un continuum de valeurs pour l'argument (au lieu des seules possibilités +1 et -1 dans le cas réel), associée au type spécial de "relation" locale entre points voisins imposée par la dérivabilité complexe, obligent une "rigidisation" du graphe de la fonction dans le cas complexe.
S@N-SaYaN M@n a écrit:Merci beaucoup, j'aimerai aussi savoir,
Quel est le rapport entre ce principe du maximum et
1) : le principe du maximum d'entropie
2) : le principe du maximum utilisé en théorie des EDP, pour montrer l'unicité des solutions (principe fort, principe faible)
S@N-SaYaN
Pour 1) je ne sais pas. Pour 2) je pense cela provient des rapports que tout ceci entretient avec les fonctions harmoniques: les solutions de l'équation de Laplace, les fonctions harmoniques, possèdent la propriété de la valeur moyenne et vérifient le principe du maximum.
Le principe du maximum n'est pas uniquement vrai pour les fonctions holomorphes complexes.
C'est un principe qui est vrai pour une large classe de fonctions (par exemple les fonctions sous harmoniques)
f vérifie le principe du maximum (en général) si f atteint son maximum sur X implique que f atteint son maximum sur la frontière de X. (ie pas dans l'intérieur de x)
C'est par exemple le cas des fonctions convexes.
A+
C'est un principe qui est vrai pour une large classe de fonctions (par exemple les fonctions sous harmoniques)
f vérifie le principe du maximum (en général) si f atteint son maximum sur X implique que f atteint son maximum sur la frontière de X. (ie pas dans l'intérieur de x)
C'est par exemple le cas des fonctions convexes.
A+
Bonsoir je profite de ce sujet sur le principe du maximum, pour vous demander si vous sauriez comment résoudre l'exercice suivant:
 est une fonction de
est une fonction de  dans
dans  dérivable au sens complexe en tout point. Montrer que le maximum de
dérivable au sens complexe en tout point. Montrer que le maximum de 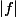 sur un compact
sur un compact  est atteint sur
est atteint sur 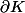 .
.
Ca n'est rien d'autre que ce fameux principe du maximum mais je n'arrive pas à passer de la dérivabilité au caractère holomorphe puis à l'analyticité.
Ca n'est rien d'autre que ce fameux principe du maximum mais je n'arrive pas à passer de la dérivabilité au caractère holomorphe puis à l'analyticité.
sept-épées a écrit:Pour une fonction d'une variable complexe, ce sont trois mots pour la même chose...
...oui mais complètement hors-programme en MP*...
La démonstration n'est pas évidente, ça m'étonnerait que ce soit ce qu'il faut faire pour résoudre l'exercice. Tu le sors d'où cet exercice ? S'il a été donné à un concours ils ont dû admettre que la dérivabilité au sens complexe impliquait l'analyticité (et faire démontrer le principe du maximum¹ avant en utilisant l'analyticité), ce n'est pas faisable sinon.
J'ai regardé dans mon cours d'analyse complexe, pour démontrer ce théorème on a utilisé l'analyticité (qui implique que si le module atteint son maximum en z0, l'ensemble des points au voisinage desquels f(z) = f(z0) est ouvert et fermé dans l'intérieur de K) et le principe du maximum pour dire que cet ensemble est non vide.
¹ celui qui dit que si f est holomorphe et |f| admet un maximum local en a, f est constante au voisinage de a, pas celui qu'il faut montrer dans l'exercice
abcd22 a écrit:...oui mais complètement hors-programme en MP*...
La démonstration n'est pas évidente, ça m'étonnerait que ce soit ce qu'il faut faire pour résoudre l'exercice. Tu le sors d'où cet exercice ? S'il a été donné à un concours ils ont dû admettre que la dérivabilité au sens complexe impliquait l'analyticité (et faire démontrer le principe du maximum¹ avant en utilisant l'analyticité), ce n'est pas faisable sinon.
J'ai regardé dans mon cours d'analyse complexe, pour démontrer ce théorème on a utilisé l'analyticité (qui implique que si le module atteint son maximum en z0, l'ensemble des points au voisinage desquels f(z) = f(z0) est ouvert et fermé dans l'intérieur de K) et le principe du maximum pour dire que cet ensemble est non vide.
¹ celui qui dit que si f est holomorphe et |f| admet un maximum local en a, f est constante au voisinage de a, pas celui qu'il faut montrer dans l'exercice
Oral de l'X 2005, pas très rassurant...
Il y a une question avant celle-ci qui demande de montrer la meme chose mais pour une série entière, en introduisant l'intégrale
Je pense que l'objectif doit etre de se ramener à ce cas simple.
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
