Bonjour,
Je n'arrive pas à montrer que la primitive de ln(1+x) = (1+x)*ln(1+x)-x. J'ai fait un changement de variable et une intégration par partie et je trouve : primitive de ln(1+x) = (1+x)*ln(1+x) - (1+x).
Je ne trouve pas mon erreur.... Pouvez vous m'aider? Merci.
Primitive de ln (1+x)
7 messages
- Page 1 sur 1
Re: primitive de ln (1+x)
Bonsoir,
effectivement une primitive de ln(1+x), avec 1+x > 0 est (x+1) ln(1+x)-x
IPP avec=u, \dfrac{dx}{1+x}=du,~~v=x)
dx=xln(1+x)-\int\dfrac{x}{1+x}dx)
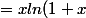-\int\dfrac{1+x}{1+x}dx+\int\dfrac{1}{1+x} dx)
....
effectivement une primitive de ln(1+x), avec 1+x > 0 est (x+1) ln(1+x)-x
IPP avec
....
Re: primitive de ln (1+x)
Ah d'accord. Je ne savais pas qu'il fallait décomposer l'intégrale de l'intégration par partie. Merci!
Re: primitive de ln (1+x)
Salut,
"Je ne trouve pas mon erreur" ...
C'est parce qu'il n'y en a pas.
Une primitive est définie à une constante près.
Et donc F1(x) = (1+x)*ln(1+x)-x et F2(x) = [(1+x)*ln(1+x)-x -1] sont toutes deux des primitives de f(x) = ln(1+x)

"Je ne trouve pas mon erreur" ...
C'est parce qu'il n'y en a pas.
Une primitive est définie à une constante près.
Et donc F1(x) = (1+x)*ln(1+x)-x et F2(x) = [(1+x)*ln(1+x)-x -1] sont toutes deux des primitives de f(x) = ln(1+x)
Re: primitive de ln (1+x)
Salut Black Jack,
certes, mais la méthode de résolution que j'ai donnée est la plus classique
certes, mais la méthode de résolution que j'ai donnée est la plus classique
Re: primitive de ln (1+x)
Salut pisigma,
Il n'y a pas de soucis avec la résolution via une simple IPP ... en effet des plus classiques.
Il me semble cependant que d'avoir rappelé à lightone que des primitives sont définies à une constante près est au moins aussi important ... et à ne plus jamais oublier.

Il n'y a pas de soucis avec la résolution via une simple IPP ... en effet des plus classiques.
Il me semble cependant que d'avoir rappelé à lightone que des primitives sont définies à une constante près est au moins aussi important ... et à ne plus jamais oublier.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
