Primitive de 1/(x²+x+1)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kmikazi
- Membre Relatif
- Messages: 143
- Enregistré le: 01 Mai 2013, 22:25
-
 par kmikazi » 21 Juin 2013, 18:56
par kmikazi » 21 Juin 2013, 18:56
bonjour, je n'arrive pas a trouver cette primitive
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 21 Juin 2013, 19:00
par Luc » 21 Juin 2013, 19:00
kmikazi a écrit:bonjour, je n'arrive pas a trouver cette primitive
Bonjour,
une technique qui marche à chaque fois que tu as un polynôme de degré 2 au dénominateur:
tu mets sous forme canonique x^2+x+1=(x+1/2)^2+...
et tu sais primitiver 1/(1+x^2) avec l'arctangente.
-
kmikazi
- Membre Relatif
- Messages: 143
- Enregistré le: 01 Mai 2013, 22:25
-
 par kmikazi » 21 Juin 2013, 19:14
par kmikazi » 21 Juin 2013, 19:14
Luc a écrit:Bonjour,
une technique qui marche à chaque fois que tu as un polynôme de degré 2 au dénominateur:
tu mets sous forme canonique x^2+x+1=(x+1/2)^2+...
et tu sais primitiver 1/(1+x^2) avec l'arctangente.
ok merci mais le 3/4 il va ou?
-
kmikazi
- Membre Relatif
- Messages: 143
- Enregistré le: 01 Mai 2013, 22:25
-
 par kmikazi » 21 Juin 2013, 19:47
par kmikazi » 21 Juin 2013, 19:47
vous etes ou? :zen:
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 21 Juin 2013, 19:56
par Joker62 » 21 Juin 2013, 19:56
Hello,
Un changement de variable en posant u = x + 1/2 ?
-
kmikazi
- Membre Relatif
- Messages: 143
- Enregistré le: 01 Mai 2013, 22:25
-
 par kmikazi » 21 Juin 2013, 20:03
par kmikazi » 21 Juin 2013, 20:03
qqn peut m'aider, je suis pommé.
-
kmikazi
- Membre Relatif
- Messages: 143
- Enregistré le: 01 Mai 2013, 22:25
-
 par kmikazi » 21 Juin 2013, 20:07
par kmikazi » 21 Juin 2013, 20:07
faut fair 2 changements de variables c'est ça?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 21 Juin 2013, 20:07
par Luc » 21 Juin 2013, 20:07
kmikazi a écrit:qqn peut m'aider, je suis pommé.
Il faut utiliser qu'une primitive de 1/(x^2+a^2) est 1/a*arctan(x/a) (pour a non nul).
Ce résultat + un petit changement de variable et c'est bon normalement.
-
kmikazi
- Membre Relatif
- Messages: 143
- Enregistré le: 01 Mai 2013, 22:25
-
 par kmikazi » 21 Juin 2013, 20:10
par kmikazi » 21 Juin 2013, 20:10
Luc a écrit:Il faut utiliser qu'une primitive de 1/(x^2+a^2) est 1/a*arctan(x/a) (pour a non nul).
Ce résultat + un petit changement de variable et c'est bon normalement.
tu m'embrouille encore plus :marteau:
le a c'est 1/2 ou 3/4?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 21 Juin 2013, 20:55
par Luc » 21 Juin 2013, 20:55
kmikazi a écrit:tu m'embrouille encore plus :marteau:
le a c'est 1/2 ou 3/4?
c'est
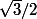
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 22 Juin 2013, 05:11
par fibonacci » 22 Juin 2013, 05:11
-
Black Jack
 par Black Jack » 22 Juin 2013, 07:59
par Black Jack » 22 Juin 2013, 07:59
A partir de x²+x+1 = (x + 1/2)² + 3/4 ...
faire le changement de variable : (x+1/2) = ((V3)/2).t
dx = ((V3)/2).dt
et on arrive à : S dx/(x²+x+1) = ((V3)/2) S dt/[(3/4)t² + (3/4)) = (2/V3). S dt/(1+t²) = (2/V3). arctg(t) = (2/V3).arctg((2/V3).(x + 1/2))
F(x) = (2/V3).arctg((2/V3).(x + 1/2)) est une primitive de f(x) = 1/(x²+x+1)
:zen:
-
kasmath
- Membre Relatif
- Messages: 186
- Enregistré le: 24 Mai 2009, 22:38
-
 par kasmath » 22 Juin 2013, 14:28
par kasmath » 22 Juin 2013, 14:28
en générale pour les fct
=\frac{1}{ax^2+bx+c})
on met le changement de variable suivant
^2)}(x+\frac{b}{2a}))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
