Bonjour,
J'essaie de trouve quelle est la primitive de la fonction :
V(aX²+bX+c)
Avec a, b et c trois réels strictement positifs et b²-4ac < 0. (il n'y a pas de solution pour aX²+bX+c = 0, et aX²+bX+c est strictement positif)
J'ai essayé l'intégration par partie en posant :
V(aX²+bX+c) = 1 x V(aX²+bX+c) ou
V(aX²+bX+c) = (2/3) x (3/2) x (2aX+b) x (1/(2aX+b)) x V(aX²+bX+c)
Et en "disant" que : (3/2) x (2aX+b) x V(aX²+bX+c)
est la primitive de : V(aX²+bX+c)^3
J'arrive à des choses que je ne sais pas résoudre...
Merci d'avance !!
Primitive/Intégrale de la racine carrée d'un polynôme du sec
12 messages
- Page 1 sur 1
Merci, mais je ne sais pas comment on sort q si il est en addition sous la racine...
Bref sous la forme canonique j'ai (d delta):
f(x) = V( [COLOR=Red]a[ [COLOR=Blue](x+b/2a)² - d/4a²][/COLOR] )[/COLOR]
d/4a² < 0 d'après mes conditions initiales, doncje ne peux pas utiliser la troisième identité remarquable... De toute façon je ne sais pas ce que j'en aurais fais...
Donc: Comment on sort + (V(-d)/2a)² de la racine ???
Bref sous la forme canonique j'ai (d delta):
f(x) = V( [COLOR=Red]a[ [COLOR=Blue](x+b/2a)² - d/4a²][/COLOR] )[/COLOR]
d/4a² < 0 d'après mes conditions initiales, doncje ne peux pas utiliser la troisième identité remarquable... De toute façon je ne sais pas ce que j'en aurais fais...
Donc: Comment on sort + (V(-d)/2a)² de la racine ???
Guillaume19 a écrit:Bonjour.
La solution final a ton probleme est
-(b^2-4xaxc)xln(2xV((aX)^2+bX+c)+2aX+b)/8V(a^3) + (2aX+b)V(aX^2+bX+c)/4a
Aprés je n'arrive pas a trouvé ce résultat sans aide.
Mais peu etre que cela va te mettre la puce a l'oreille !!xD
C'est a² x X² ou aX² ???
Sinon meric pour votre aide, quand j'aurrais autre chose q'une feuille de 10 cm sur 20 cm, je poserais tout ça pour voir ce qu'il se passe...
Au fait, est-ce que le changement de variable ne m'empèche pas de trouver la primitive ?? (je ne veux pas seulement intégrer, c'est la primitive qui m'intéresse...)
Merci d'avance.
valentin.b a écrit:Au fait, est-ce que le changement de variable ne m'empèche pas de trouver la primitive ?? (je ne veux pas seulement intégrer, c'est la primitive qui m'intéresse...)
Non, un changement de variable
J'ai donc:
On fait le changement de variable :
On a : (la lettre grec je la note O)
O(u) = X
Donc
u = O(-1) (X) (la réciproque)
Ce qui fait que :
O(u) = (V(-d)/2a) x (u - b/V(-d))
dO(u)/du = V(-d)/2a
Intégrale de [la réciproque des bornes,
( V(-d)/4a² ) x V((O(-1)(O(u)))²+1) x O'(u) x du ]
= Intégrale de [la réciproque des bornes,
( V(-d)/4a² ) x V(u²+1) x V(-d)/2a x du ]
= Intégrale de [la réciproque des bornes,
( -d/8a^3 ) x V(u²+1) x du ]
C'est pas trop faux jusque là ?
On fait le changement de variable :
On a : (la lettre grec je la note O)
O(u) = X
Donc
u = O(-1) (X) (la réciproque)
Ce qui fait que :
O(u) = (V(-d)/2a) x (u - b/V(-d))
dO(u)/du = V(-d)/2a
Intégrale de [la réciproque des bornes,
( V(-d)/4a² ) x V((O(-1)(O(u)))²+1) x O'(u) x du ]
= Intégrale de [la réciproque des bornes,
( V(-d)/4a² ) x V(u²+1) x V(-d)/2a x du ]
= Intégrale de [la réciproque des bornes,
( -d/8a^3 ) x V(u²+1) x du ]
C'est pas trop faux jusque là ?
abcd22 a écrit:C'est égal à. Ensuite on pose
, ou directement
pour tout faire en une fois.
Je viens tout juste d'avoir mon bac, et le sinus hyperbolique je ne connais que de nom (même si la réciproque et la dérivée sont trouvables sur internet).
C'est quoi en fait ?
J'ai vu un truc sur internet où il parle d'une fonction complexe... Je veux résoudre mon problème sur lR.^^
valentin.b a écrit:= Intégrale de [la réciproque des bornes,
( -d/8a^3 ) x V(u²+1) x du ]
J'ai -d/(4a^(3/2)) comme constante, tu as multiplié une fois de trop par la dérivée non ? La dérivée apparaît dans le changement de variable parce que si
Larticle wikipedia présente le sinus hyperbolique sur C, mais on peut le restreindre aux réels, et dans ce cas cest une bijection strictement croissante de R. La réciproque s'appelle arcsinh (ou argsh) et elle peut aussi sécrire comme un logarithme (on résout l'équation en x y = sinh(x) en remplaçant sinh par sa définition et en se ramenant à un trinôme en e^x). Il y a aussi le cosinus hyperbolique cosh, et on a pour tout réel x
Si c'est pas trop chiant, tu peux me montrer comment on fais pour le changement de variable... Je ne maitrise pas du tout ça.
Sinon après je crois comprendre qu'il faut poser u = sinh(t) ce qui donnera
V(1+sinh(t)) = Vcosh(t)... Enfin je sais pas trop.
Merci d'avance pour la demonstration pour le changement de variable ^^'...
Sinon après je crois comprendre qu'il faut poser u = sinh(t) ce qui donnera
V(1+sinh(t)) = Vcosh(t)... Enfin je sais pas trop.
Merci d'avance pour la demonstration pour le changement de variable ^^'...
Bon on se retrouve avec une intégrale de la forme 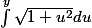 , il y a une constante devant que jai enlevée et y est un truc compliqué qui dépend de x. On pose
, il y a une constante devant que jai enlevée et y est un truc compliqué qui dépend de x. On pose 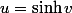 (soit
(soit 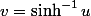 ), donc
), donc 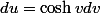 . On obtient
. On obtient 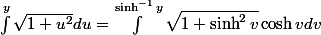 , comme 1 + sinh² = cosh² (et cosh est toujours positif), ça donne
, comme 1 + sinh² = cosh² (et cosh est toujours positif), ça donne 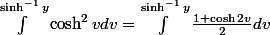 , pour la dernière égalité on prend la définition de cosh avec les exponentielles et on développe le carré, cest pareil que quand on utilise les formules dEuler avec les sin et cos (en fait on peut déduire les formules trigo hyperboliques de celles avec sin et cos), et là cest facile à calculer.
, pour la dernière égalité on prend la définition de cosh avec les exponentielles et on développe le carré, cest pareil que quand on utilise les formules dEuler avec les sin et cos (en fait on peut déduire les formules trigo hyperboliques de celles avec sin et cos), et là cest facile à calculer.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
