Pour produit direct montrer l'unicité du morphisme h

[adexvectorquantic]

Bonjour,
est un morphisme universel si et seulement pour tous morphismes et pour tout objet il existe un unique morphisme (dont les domaines de départ et arrivée sont donnée dans la figure ci-contre) tel que le diagramme commute.


J'ai réussi (je cherche à démontrer que est bel et bien un morphisme universel) à démontrer l'existence d'un tel . Mais j'ai du mal avec l'unicité.

Voici une amorce de ma démonstration pour l'unicité :

Supposons qu'il existe deux qui conviennent.
On aurait du coup :

Je suis quasiment sûr que l'on a
Je ne sais juste pas comment le démontrer (je saurais avec des projecteurs orthogonaux...)

Merci par avance.
Bonne journée

PS : sont des objets de la catégorie étudiée et est l'opérateur diagonal.

[Ben314]

Salut,
Je comprend pas grand chose :
- Si tu travaille avec des catégories quelconques, c'est quoi ton + dans ?
- C'est quoi ton "opérateur diagonal" : si est un éléments de ta catégorie, c'est quoi ?

P.S. Je précise, au cas où le problème soit un problème de vocabulaire, que ce que j'ai pris comme définition d'une "catégorie", c'est ce qu'on trouve par exemple là :
https://fr.wikipedia.org/wiki/Th%C3%A9o ... 3%A9gories

[adexvectorquantic]

Bonjour,

, c'est un fonctor de la catégorie vers .

Pour ce qui est de j'ai dû prendre une mauvaise piste ... Vous avez raison il n'y a pas d'addition possible.

[Ben314]

D'un autre coté, je comprend pas non plus ce que tu cherche à démontrer :
Au début ça donne l'impression que tu cherche à montrer que le problème universel admet bien une unique solution, donc que quelque soit et il existe un unique couple tel que bla bla bla.
Sauf que dans la suite, ce que tu cherche à montrer, on dirait que c'est l'unicité de ce qui, me semble t-il, signifie que et , tu les connait déjà et que tu veut vérifier qu'ils sont solution du problème universel. . .
Bref, c'est qui le et le que tu manipule dans ta prose ?

[adexvectorquantic]

A vrai dire j'ai appris la définition d'un morphisme universel (qui est soit un morphisme initial soit un morphisme terminal) à partir du Wiki anglais.

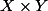
Dans ma question, le couple et () est un morphisme terminal (de vers ).

J'entends par là que ce couple est tel que pour tout et il existe un unique morphisme (dont les domaines de départ et arrivée sont donnés dans le diagramme) tel que le diagramme commute.

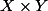
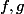
Je cherche donc à démontrer que le couple et () est un morphisme terminal. Pour cela je dis : soient deux morphismes quelconques, soit un objet quelconque et montrer qu'il existe un unique tel que le diagramme commute.

Pour répondre à votre commentaire, font partie du morphisme universel. En tout cas, d'après la définition anglosaxone... Qui est celle avec laquelle j'ai débuté.

[Ben314]

Je cherche donc à démontrer que le couple et () est un morphisme terminal. . .

Certes, mais c'est qui et ?

[adexvectorquantic]

Ah oui pardon, et sont les projections sur et de .

Désolé!

[Ben314]

C'est toujours pas super clair vu que, de la façon dont je le comprend, il me semble que c'est la définition même du produit de deux objets de la catégorie que tu as.
Donc, soit tu es dans le cas général des catégories et ce fameux produit peut exister ou ne pas exister selon la catégorie, soit tu es dans un cas particulier de catégorie où tu veut montrer que le produit va exister et il faudrait que tu précise la catégorie.