Produit direct
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 31 Oct 2014, 22:57
par barbu23 » 31 Oct 2014, 22:57
Pour comprendre l'origine du fait que
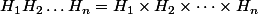
, il vaut mieux lui trouvr une analogie avec le cas des espaces vectoriels.
Si

est un espace vectoriel de dimension finie et
_{i=1, \dots , k})
une famille de sous espaces vectoriels, avec
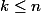
, alors :
la famille
_{i=1, \dots , k})
est en somme directe dans

, si :
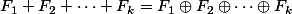
, et cela d'après l'algèbre linéaire ne peut avoir lieu que si :
 \bigcap F_{i+1} = \{ 0_E \})
pour tout

. ( Cela se trouve dans n'importe quel cours d'algèbre linéaire de niveau ;

).
Cordialement. :happy3:

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 01 Nov 2014, 17:48
par capitaine nuggets » 01 Nov 2014, 17:48
barbu23 a écrit:Pour comprendre l'origine du fait que
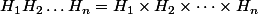
barbu23 a écrit:la famille
_{i=1, \dots , k})
est en somme directe dans

, si :
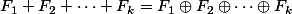
Ce serait pas plutôt

?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 01 Nov 2014, 17:52
par barbu23 » 01 Nov 2014, 17:52
Oui. :happy3:
Mais, dans la plupart du temps, on écrit :

au lieu de la notation que tu choisis. :happy3:
-
Leccornia
- Messages: 4
- Enregistré le: 04 Nov 2014, 17:58
-
 par Leccornia » 04 Nov 2014, 18:04
par Leccornia » 04 Nov 2014, 18:04
Bonsoir,
J'ai regardé toute les réponses sur cette page au sujet de votre question mais je n'ai pas compris. Comment montre t-on que si G est abélien fini et si x^p=1 avec p premier alors G=H1.H2...Hn? Et quel est l'ordre des Hi? p?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 04 Nov 2014, 18:40
par Ben314 » 04 Nov 2014, 18:40
Ben314 a écrit:On prend
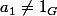
, puis

puis

, etc..
et

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 07 Nov 2014, 00:35
par barbu23 » 07 Nov 2014, 00:35
Bonsoir à tous,
On sait qu'il y'a équivalence entre la notion de groupe abélien et la notion de

- module.
Existe -t-il une équivalence entre la notion de groupe
non abélien et la notion de module à gauche et module à droite ?
Merci d'avance. :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Nov 2014, 11:23
par Ben314 » 07 Nov 2014, 11:23
RAPPEL : Quelque soit l'anneau A, un A-module M, c'est un ensemble muni d'une loi de groupe
commutative notée + et... d'autres trucs...

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
... C'est simplement l'application d'un théorème qui se trouve ici : http://fr.wikipedia.org/wiki/Produit_direct_%28groupes%29 . ( Lis la partie ( paragraphe ) : Produit direct interne d'une famille finie de sous-groupes )
