Polyômes cyclotomiques

[rain]

Bonjour, je n'arrive pas à comprendre une majoration concernant un polynôme cyclotomique, et donc j'aimerai de l'aide.
( c'est un produit où k est l'indice)
avec le nième polynome cyclotomique
q dans, une racine primitive de l'unité, l'indicateur d'Euler et k un entier inférieur ou égale à n>1, premier avec n.
J'espère que c'est claire, j'ai fais des recherches et j'ai vu qu'il y a un truc avec un triangle dans la cercle trigo, mais je comprends pas.

[mathelot]

Bonjour, je n'arrive pas à comprendre une majoration concernant un polynôme cyclotomique, et donc j'aimerai de l'aide.
( c'est un produit où k est l'indice)
avec le nième polynome cyclotomique
q dans, a une racine primitive de l'unité, l'indicateur d'Euler et k un entier inférieur ou égale à n>1, premier avec n.
J'espère que c'est claire, j'ai fais des recherches et j'ai vu qu'il y a un truc avec un triangle dans la cercle trigo, mais je comprends pas.

je me demande si ces inégalités ne sont pas triviales pour :

celle de gauche , c'est un produit de

celle de droite, ce sont des distances entre nombres complexes
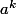
q est sur l'axe réel, des affixes de point sur le cercle trigo, 1 est l'affixe du point extremal à droite du cercle trigo,
donc le plus proche du point d'affixe q (lui sur l'axe réel) dans le plan complexe ??

[rain]

Pour l'inégalité de droite OK, mais à gauche çà me paraît pas évident. sur wikipedia article polynôme cyclotomique il y a un truc de triangle pour le démontrer. Et aussi je comprends ta démonstration sauf la dernière phrase, je vois pas comment démontrer l'inégalité à partir d'elle.

[rain]

OK c'est bon, merci.

[ThSQ]

Ça sent le théorème de Wedderburn .... :id:

[rain]

Ça sent le théorème de Wedderburn .... :id:

C'est çà, je doit faire la démonstration.