Polynômes et suites
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 16 Sep 2007, 18:46
par pouik » 16 Sep 2007, 18:46
Bonsoir,
Pour tout
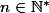
, soit

la fonction polynôme définie par
 = x^n + x - 3)
. Montrer que, pour tout
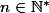
,

admet une unique racine réelle positive, que l'on notera

. Montrer que
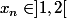
. Déterminer le signe de
)
, en déduire que la suite
)
est décroissante.
Et donc en fait je n'arrive pas du tout à traiter la toute première tache demnadée....


Pouvez vous m'aider ?? Merci par avance.
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 16 Sep 2007, 18:51
par Quidam » 16 Sep 2007, 18:51
Si tu calculais la dérivée de
)
, ne pourrais-tu pas en déduire un tableau de variation sur
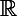
?
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 16 Sep 2007, 18:58
par pouik » 16 Sep 2007, 18:58
On a
 = nx^{n-1} + 1)
mais comment puis-je faire pour avoir le tableau de variationsune fois à ce stade ?
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 16 Sep 2007, 19:05
par Quidam » 16 Sep 2007, 19:05
pouik a écrit:On a
 = nx^{n-1} + 1)
mais comment puis-je faire pour avoir le tableau de variationsune fois à ce stade ?
Le tableau de variation s'établit avec le signe de la dérivée ! Ne peux-tu déterminer le signe de
 = nx^{n-1} + 1)
? Quand même !
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 16 Sep 2007, 19:10
par pouik » 16 Sep 2007, 19:10
Tout dépend de la parité de n, si n est est impair la dérivée est positive, mais si n est pair je ne vois pas comment faire... :triste: :triste:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 16 Sep 2007, 19:17
par fahr451 » 16 Sep 2007, 19:17
l 'énoncé est ambigu
est ce qu 'on cherche les racines réelles ou a priori réelles positives
il faut comprendre le deuxième cas
on se place A PRIORI sur R+ et on cherche les racines
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 16 Sep 2007, 19:27
par pouik » 16 Sep 2007, 19:27
ah donc si on est sur R+,

est strictement croissante et comme elle est bijective et que
 = -3)
on en déduit d'après le TVI que

admet une unique racine réelle positive.
Est-ce bien ca, ou ai-je étéun peu vite en conjecture ?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 16 Sep 2007, 21:44
par fahr451 » 16 Sep 2007, 21:44
ça semble bien
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités