Polynomes primitifs de F2[X] [Résolu]

par **zenaf** » 17 Déc 2009, 10:57

Bonjour.
Je voulais simplement savoir une condition necessaires et suffisante (ou seulement suffisante) pour qu'un polynome de F2[X] soit primitif. Doit t'il forcement etre irreductible?
Merci

par **yos** » 17 Déc 2009, 12:23

Je sais pas si ça a un sens (ou un intérêt) de parler de parler de polynôme primitif sur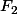

. Il faut un anneau factoriel à la base et son corps des fractions. Ceci est trop trivial pour

.
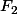Si tu prends la définition "primitif= pgcd des coefs vaut 1", tu as bien un truc sans intérêt puisque les coefs valent tous 0 ou 1.

par **zenaf** » 17 Déc 2009, 19:53

en fait il s'agit d'un polynome de rétroaction pour un LFSR. Un théoreme dit que la période d'un LFSR est maximale lorsque le polynome de rétroaction associé est primitif dans F2[X]. D'ou la question :hein:

par **Nightmare** » 17 Déc 2009, 20:05

Salut :happy3:

Il me semble qu'on peut parler de polynôme primitif sans parler de pgcd : Un polynôme sur un anneau commutatif unitaire A est primitif si A est le plus petit idéal principal contenant les coefs du polynôme.

par **Nightmare** » 17 Déc 2009, 20:06

Concernant la caractérisation, j'ai trouvé sur le net que ton polynôme sera primitif si le plus petit entier n tel que P divise x^n - 1 est égal à

(Dans

premier, on remplace 2 par p)

par **zenaf** » 17 Déc 2009, 20:31

merci beaucoup nightmare pour ta reponse. Je crois que ca merite un petit "Résolu" ^^

par **wserdx** » 17 Déc 2009, 23:00

Je rajouterai simplement qu'un polynôme primitif de

de degré

est par définition le polynôme minimal sur

d'un élément primitif de

.
Un polynôme primitif est donc nécessairement irréductible. (mais ce n'est pas une condition suffisante)
Je confirme la caractérisation donnée par Nightmare.

par **yos** » 18 Déc 2009, 11:44

Nightmare a écrit: Il me semble qu'on peut parler de polynôme primitif sans parler de pgcd : Un polynôme sur un anneau commutatif unitaire A est primitif si A est le plus petit idéal principal contenant les coefs du polynôme.

Définition trivialisante comme je le disais car

n'a que deux idéaux.

Nightmare a écrit:j'ai trouvé sur le net que ton polynôme sera primitif si le plus petit entier n tel que P divise x^n - 1 est égal à 2^{deg P}-1 .

Intéressant, mais apparemment sans rapport avec la définition générale des polynômes primitifs basée sur la notion de contenu.

Polynomes primitifs de F2[X] [Résolu]

Polynomes primitifs de F2[X] [Résolu]

Qui est en ligne