Effectivement, je n'avais pas relevé cette propriété dans mon cours. À quoi est-elle due exactement ?
Voilà ce que j'ai trouvé :
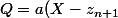(X-z_n)...(X-z_1) \\<br />Q=a(X^{n+1}+\sum_{k=1}^{n+1}z_k \cdot X^n + K + (-1)^{n+1} \prod_{k=1}^{n+1} \cdot z_k))
avec K appartient à IK[X], val(K) = 1 ou 2 ou ... ou n-1 et deg(K) = n-1 ou n-2 ... ou 1 ou bien K est le polynome nul.
Par identification, on a donc a = n, SOMME = (n+1)/n et PRODUIT = (-1)^(n+1)/n et K = 0
Voici la suite de l'énoncé : « 2) On choisit n=3 dans cette question seulement. Écrire la formule de Taylor pour Q en 1. »
}( \alpha )}{k!} \cdot (X - \alpha))
« 3) Montrer que 1 est une racine d'ordre 2 de Q. »
Q(1) = n-(n+1)+1 = 0
Donc 1 est une racine de Q.
Q' = n(n+1)X^n - n(n+1)X^(n-1)
Q'(1) = n(n+1) - n(n+1) = 0
Donc 1 est une racine d'ordre 2 de Q.
Une petite question à propos ce ça. 1 est une racine d'ordre 2 signifie-t-il qu'elle est au moins double ? En gros, ma question, c'est si une racine est d'ordre n+1, est-elle aussi d'ordre n ?
« 4) Montrer que (X-1)²P' = Q »
C'est bon.
« 5) Soit alpha une racine nième de 1. Calculer la somme
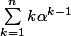
en fonction de n et alpha (sans exposants) »
pfft :mur:
Merci de ton aide

.
Hick_Jeck
