Bonjour,
Vu l'énoncé, je chercherais effectivement du côté des polynômes et vu que tu as quatre conditions je pense qu'un polynôme

de degré 3 fera l'affaire.
Je te conseille d'abord d'utiliser la transformation
=P(X+t_0)-u_0)
, comme ça tu as
=Q'(0)=0)
, donc
=X^2(aX+b))
. Ensuite tes deux autres conditions deviennent

et
+b=\frac{u_1-u_0}{(t_1-t_0)^2})
.
Si je ne me trompe pas dans les calculs (ça peut arriver à 3h du matin...), tu dois avoir
^2}+\frac{u_0}{t_0^2}\right])
et
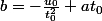
.
Enfin il reste à faire la transformation inverse
=Q(X-t_0)+u_0)
si tu veux une formule explicite.
Si tu veux mettre tout ça sur ordinateur, le plus simple est de faire
Python
- Code: Tout sélectionner
t0, t1, u0, u1 = # Variables
# Je mets a et b ici comme ça elles sont calculées une seule fois
a = 1 / t1 * ((u1 - u0) / (t1 - t0) ** 2 + u0 / t0 ** 2)
b = -u0 / t0 ** 2 + a * t0
def P(t):
return (t - t0) ** 2 * (a * (t - t0) + b) + u0
Si tu veux tu peux aussi tout encapsuler dans une fonction qui dépend des variables.
Tu peux aussi trouver des polynômes de degré supérieur, mais les équations à résoudre pour en déterminer les coefficients deviennent compliquées à résoudre à la main. Pour ça tu peux utiliser des solveurs inclus dans Scipy sour Python par exemple.
J'espère ne pas me tromper sur les formules (vérifie-les au cas où) et bon courage pour ton TIPE!
PS : Juste par curiosité, il porte sur quoi ton TIPE ?
