TIPE en mpsi : topologie

par **Hugow** » 22 Avr 2009, 19:29

Bonsoir ! Je suis actuellement en maths sup et pour les TIPE, nous avons travaillé mon groupe et moi-même sur quelques notions de base de topologie.

Nous nous sommes intéressés à la preuve suivante :

Soit E un espace topologique, A et B deux parties fermées de E telles que AUB et A;)B soient connexes par arcs ALORS A et B sont connexes par arcs.

Nous avons essayé d'adapter cette preuve à la connexité simple. Voila notre preuve :

On suppose AUB connexe

prenons a

A, donc a

AUB

Or AUB est connexe quelle que soit f continue, quel que soit x

AUB

f(x)=;)f

or a

AUB => quel que soit x

A, f(x)=f(a)=;)f => A connexe

Tient-elle la route à votre avis ?
Merci de vos réponses :we:

par **Nightmare** » 22 Avr 2009, 19:54

Salut :happy3:

Je ne comprends pas vraiment ta preuve...

Ok, si on considère f continue de A dans {0,1} alors elle est constante sur AUB. Mais tu n'as pas prouvé qu'elle était constante sur A tout entier !

Voici une démonstration un peu plus sûre :

Supposons que A puisse s'écrire comme réunion de deux fermés X et Y.

et

sont deux fermés de

.

Or,

et on en déduit qu'un des deux est vide.

Montrons qu'alors X et Y sont vides.

et

sont fermés dans

.
Or,

et comme ce dernier est connexe,

ou

, ie

CQFD.

par **busard_des_roseaux** » 22 Avr 2009, 21:23

Bs,

un exemple célèbre:

Dans le plan, la réunion de l'axe y'oy et de la famille des droites
horizontales d'équation y=

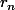
où

est connexe par arcs mais non localement connexe par arcs.

en effet, on connexifie la famille de droites via l'axe y'oy , c'est à dire
pas de manière locale.

par **Hugow** » 24 Avr 2009, 19:18

Merci beaucoup pour vos réponses rapides !

Nous allons essayer de travailler cet aspect de notre tipe à la lueur de vos éclaircissements :happy2: merci !

par **leon1789** » 25 Avr 2009, 14:51

La preuve de Hugow est incorrecte car il ne précise pas où la fonction f est continue : sur A, sur A U B ?? ...

Nightmare a écrit:Supposons que A puisse s'écrire comme réunion de deux fermés X et Y.

Je suppose que tu veux dire réunion disjointe.

Nightmare a écrit: et sont deux fermés de .

Tu veux surement dire

. Je corrige dans la suite...

Nightmare a écrit:Or, et on en déduit qu'un des deux est vide.

ok, parce que réunion disjointe.

Nightmare a écrit:Montrons qu'alors X et Y sont vides.

Tu veux dire >.

Nightmare a écrit: et sont fermés dans .
Or, et comme ce dernier est connexe, ou , ie

CQFD.

Ici, tu as supposé

, c'est bien ça ?
ok.

par **Nightmare** » 25 Avr 2009, 15:07

Oui merci pour la correction de mes petites étourderies.

par **Nightmare** » 25 Avr 2009, 15:20

Je pense qu'on doit pouvoir se dépatouiller pour trouver une preuve utilisant la continuité.

On veut montrer que f : A -> {0,1} est toujours continue. Comme A est connexe par arcs il suffit donc de montrer qu'elle est localement continue. Ca doit se faire sachant que sa restriction sur

et qu'un prolongement sur

sont constants par connexité.

Je n'ai pas le temps j'y réfléchis quand je reviens.

par **leon1789** » 25 Avr 2009, 15:26

Nightmare a écrit:Oui merci pour la correction de mes petites étourderies.

:zen:

C'est compréhensible qu'il y en ait quand on va vite dans la réponse

TIPE en mpsi : topologie

TIPE en mpsi : topologie

Qui est en ligne