Polynome annulateur

[Blurk]

bonjour !
J'ai une petite question au sujet des polynômes annulateurs dans les matrices: quand on a une matrice, comment trouver un polynome annulateur? est ce que l'on prend toujours la diagonale ou pas ? comment vérifier que le polynome est annulateur ?

Par exemple sur la matrice
( 1 5 6 )
( 8 4 1 )
( 3 6 9 ) ?
merci,

[zorg]

Soit P_A(X)=det(A-XI_n) le polynôme caractéristique de A. Le théorème de Cayley-Hamilton dit que P_A est un polynôme annulateur de A.

Soit à présent mu_A(X) le polynome minimal de la matrice A. Alors un théorème nous dit que P est un polynôme annulateur de A si et seulement si le polynôme mu_A divise P.

Donc pour chercher le polynôme minimal de A, il faut chercher parmi les diviseurs de P_A(X) et vérifier que ça annule bien A.

A présent, si pour une matrice particulière, il s'agit juste de chercher UN polynôme annulateur, on peut toujours prendre le polynôme caractéristique.


Je ne comprends pas bien l'histoire de ta diagonale ??

Si on a une matrice du type , il est facile d'avoir un polynôme annulateur. La matrice N=A-aI_3 est une matrice nilpotente c'est-à-dire qu'il existe un entier k tel que N^k=0. Ici k=3. Ce qui signifie que le polynôme (X-a)^3 annule lamatrice A. En fait c'est la même chose que le polynôme caractéristique de A !!!

[Blurk]

je crois que ça commence à être un peu plus clair pour moi mais pour etre plus sur, sur l'exemple,quel serait donc un polynome annulateur?et le polynome caratéristique ?...
merci d'avance parce que tout ceci ne me parait pas encore du tout évident...

[nyafai]

pour calculer le polynome caractéristique, il te faut calculer le déterminant de la matrice
( (1-x) 5 6 )
( 8 (4-x) 1 )
( 3 6 (9-x) )
je te laisse ce plaisir :lol5: , c'est parfaitement possible avec la règle de Sarrus.
Ensuite, pour trouver des polynomes annulateurs tu peux regarder dans ses diviseurs s'il n'y en a pas un plus simple qui marche( sachant que le polynome caractéristique est déja un polynome annulateur par Cayley Hamilton). il faudra probablement essayer de trouver les racines de ton polynome caractéristique.

Souvent il y a des méthodes plus simples (comme par exemple les matrices nilpotentes que t'a montrées zorg) mais dans le cas général et comme je ne vois de particularités à ta matrice, la méthode bourrin que je viens de te donner fonctionnera toujours.
bon courage

[Blurk]

:hein: Désolée mais je ne connais pas la règle de Sarrus...et je rencontre un autre problème...une fois que j'aurais calculé le déterminant, comment dois je faire pour avoir le polynôme caractéristique ?

[nyafai]

ben le déterminant, c'est le polynome caractéristique ! c'est meme sa définition 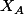: (est le polynome caractéristique)

pour la règle de Sarrus, en fait c'est juste un moyen mémotechnique pour calculer un déterminant d'ordre 3 et moi ca figurait dans mon cours sur les déterminants. En fait, ca revient plus aou moins à développer le déterminant suivant une colonne mais en ayant direct le résultat simplifié. J'ai pas regardé mais en cherchant sur wikipedia ou google tu devrais trouver ca si c'est pas dans ton cours.
bon courage !

[Blurk]

a merci j'ai trouvé pour Sarrus !
il me reste une petite question,comment fait on pour vérifier qu'un polynome annule bien une matrice ? Je ne sais pas si c'est une question bête mais je ne sais pas le faire...Pour le reste vos explications m'ont été tres utiles ! merci beaucoup !

[Diaz]

Je me demande si ta question n'était pas plutôt de savoir comment faire pour trouver le polynôme minimal d'une matrice;si j'ai cette impression,c'est parce que tu demandes comment faire pour trouver LE polynôme annulateur d'une matrice,alors que tu devrais plutôt demander comment faire pour trouber UN polynôme annulateur d'une matrice;en effet,l'article défini que tu as employé pour poser ta question laisse penser que soit tu ne maîtrise pas le sujet,soit tu voulais plutôt demander comment faire pour trouver le polynôme minimal d'une matrice:A la lumière de tout ce que je viens de te dire,peux-tu apporter des précisions à ta question? Si ta question était bien de savoir comment faire pour trouver un polynôme annulateur,alors toutes les réponses ci-dessus devraient te suffire;sache,en outre,que tout multiple d'un polynôme annulateur est un polynôme annulateur.

[nyafai]

si est un polynome annulateur de A (A une matrice), ca veut dire que
avec
et le 0 de droite correspondant à la matrice de même taille que A ne contenant que des zéros
voilou, bonne continuation

[Blurk]

Merci Nyafai ! C'est bon j'ai compris comment on pouvais vérifier qu'un polynome annulait une matrice ...merci beaucoup à tous pour votre aide !