Point adhérent et limite supérieure
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
cyril3
- Messages: 7
- Enregistré le: 10 Avr 2007, 12:37
-
 par cyril3 » 14 Oct 2007, 16:23
par cyril3 » 14 Oct 2007, 16:23
bonjour,
alors voila jdois résoudre un exercice et je ne vois pas trop comment commencer...
"Soit (xn) une suite bornée et désignons par E l'ensemble de ses points adhérents. Montrer que sup(E)=lim sup (xn) "
merci d avance
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 14 Oct 2007, 17:13
par ThSQ » 14 Oct 2007, 17:13
points adhérents = valeurs d'adhérence (de la suite) ??
-
cyril3
- Messages: 7
- Enregistré le: 10 Avr 2007, 12:37
-
 par cyril3 » 14 Oct 2007, 18:51
par cyril3 » 14 Oct 2007, 18:51
oui oui on dit que x est un point adhérent de la suite ssi on peut extraire une sous suite de (xn) qui converge vers x
-
mbodji
- Membre Naturel
- Messages: 14
- Enregistré le: 07 Juin 2006, 11:06
-
 par mbodji » 14 Oct 2007, 18:57
par mbodji » 14 Oct 2007, 18:57
puisque xn est bornée, il existe une sous suite de xn qui converge vers x appartenant à E d'apres bolzano-weirstrass, c'est une piste
-
SimonB
 par SimonB » 14 Oct 2007, 18:58
par SimonB » 14 Oct 2007, 18:58
Ecrit comme ça, je pense que c'est faux (un exemple au hasard : je prends

si n est plus grand que 1. Le sup de E, c'est 0, et la limite du sup des

, c'est 100...
 par busard_des_roseaux » 14 Oct 2007, 19:04
par busard_des_roseaux » 14 Oct 2007, 19:04
bjr,
a)

est un point adhérent.
donc
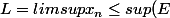)
.
b)

, il n'y a qu'un nombre fini de termes de la suite

donc:
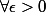
,

n'est pas un point adhérent.
donc
 \leq L +\epsilon)
d'où
 \leq L)
-
SimonB
 par SimonB » 14 Oct 2007, 19:11
par SimonB » 14 Oct 2007, 19:11
Oups, on parlait ici de la limite supérieure. Désolé, je connais très mal ce terme.
-
bruce.ml
- Membre Rationnel
- Messages: 630
- Enregistré le: 18 Juin 2007, 23:54
-
 par bruce.ml » 14 Oct 2007, 19:13
par bruce.ml » 14 Oct 2007, 19:13
SimonB a écrit:Ecrit comme ça, je pense que c'est faux (un exemple au hasard : je prends

si n est plus grand que 1. Le sup de E, c'est 0, et la limite du sup des

, c'est 100...
non simonB. Quand on parle de limite des sups, ce sont les sups d'après, on ne compte pas les valeurs d'avant :

-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 14 Oct 2007, 19:23
par barbu23 » 14 Oct 2007, 19:23
L'ensemble des points adherents à une suite
_{n \in \mathbb{N}} $)
s'écrit comme ça :


si l'ensemble dans lequel est inclus la suite
_{n \in \mathbb{N}} $)
, est compact.
Cette piste peut ,peut etre vous aider !!
-
cyril3
- Messages: 7
- Enregistré le: 10 Avr 2007, 12:37
-
 par cyril3 » 14 Oct 2007, 19:30
par cyril3 » 14 Oct 2007, 19:30
dsl mais je bloque deja sur un premier point :
qu'est ce qui nous dit que lim sup (xn) est lui même un point adhérent?
Enfin je le conçois bien mais comment le montrer?
merci
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 14 Oct 2007, 19:46
par barbu23 » 14 Oct 2007, 19:46
Attend, j'ai la demonstration de ton exo en pdf sur mon "pc" , mais je sais pas comment le faire coller ici !! Est ce que vous savez comment !!? j'ai pas envie d'écrire tout le paragraphe ici :king: , c'est un peu long !!!!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 14 Oct 2007, 19:47
par barbu23 » 14 Oct 2007, 19:47
pas, trop long, mais bon ... !!
C'est sur la page

!!
Dites moi comment faire ?!
 par legeniedesalpages » 14 Oct 2007, 20:24
par legeniedesalpages » 14 Oct 2007, 20:24
On note

, et pour tout entier n,

.
On a

,

quelque soit n.
Pour tout n,

est non vide et bornée, donc admet une borne supérieure

. On a

.

,
donc

car E est fermé borné.
Remarquons que
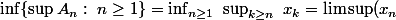)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
