La fontion "fn" est definie sur ]0,+oo[ : fn(x) = x^2 - nln(x)
1) Calculez les limites de fn(x) quand : x tend vers 0 à droite / x tend vers +oo
2) Etudiez les changements de fn et tracez le tableau de variation. (la derivée s'annule dans la racine fe n/2)
3) Etudiez la situation relative des courbes (Cn) et (Cn+1)
4) Supposons n > 6
Montrez que l'equation fn(x)=0 accept 2 solutions differents Un et Vn + (Un < Vn)
5) Calculez la limite de Vn quand n tend vers +oo
Et montrez que la limite de "(Vn^2)/(nln(n))" = 1/2 quand n tend vers +oo
La plus difficile limite
5 messages
- Page 1 sur 1
La plus difficile limite
par zerow2001 » 06 Jan 2019, 21:54
Modifié en dernier par zerow2001 le 07 Jan 2019, 13:13, modifié 2 fois.
Re: La plus difficile limite
par Ben314 » 06 Jan 2019, 23:37
Salut,
3) Pour tout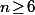
, au vue du tableau de variation de 
, on sait que 
donc 
.
De plus, par définition de
, on a \!=\!0)
c'est à dire que \!=\!0)
et on en déduit que
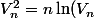>n\ln\!\big(\sqrt{\frac{n}{2}}\big)=\frac{n}{2}\ln\!\big(\frac{n}{2}\big)=\frac{n}{2}\big(\!\ln(n)\!-\!\ln(2)\big)\text{ c'est \`a dire que }\dfrac{V_n^2}{n\ln(n)}>\dfrac{1}{2}-\dfrac{\ln(2)}{2\ln(n)})
.
D'un autre coté, on a :
}\,\big)\!<br />=n\ln(n)\!-\!n\ln\big(\sqrt{n\ln(n)}\,\big)<br />=\dfrac{n}{2}\Big(\ln(n^2)\!-\!\ln\big(n\ln(n)\,\big)\Big)<br />=\dfrac{n}{2}\ln\!\bigg(\dfrac{n}{\ln(n)}\bigg)>0)
vu que)
. Le tableau de variation de montre alors que })
et on en déduit que
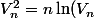<n\ln\!\big(\!\sqrt{n\ln(n)}\,\big)=\frac{n}{2}\Big(\!\ln(n)\!+\!\ln\!\big(\ln(n)\big)\Big)\text{ c'est \`a dire que }\dfrac{V_n^2}{n\ln(n)}<\dfrac{1}{2}+\dfrac{\ln\!\big(\ln(n)\big)}{2\ln(n)})
.
On conclue alors à l'aide du théorème des gendarmes.
3) Pour tout
De plus, par définition de
D'un autre coté, on a :
vu que
On conclue alors à l'aide du théorème des gendarmes.
Modifié en dernier par Ben314 le 08 Jan 2019, 01:53, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: La plus difficile limite
par pascal16 » 07 Jan 2019, 09:31
Ca ne donne pas envie de continuer à aider quand on a passé du temps à écrire un réponse et que l'énoncé disparaît.
C'est un peu le cas quand l'énoncé évolue au fil du temps.
C'est un peu le cas quand l'énoncé évolue au fil du temps.
Re: La plus difficile limite
par zerow2001 » 07 Jan 2019, 13:15
Je suis vraiment désolé mais c'était mon frère qui a supprimer l'enonce, je suis vraiment désolé Ben314 et Pascal16
désolé !
désolé !
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :