Développement limité, j'en peux plus

[ZBAR]

Bonjour à tous, je suis bloquée dans une étape d'un exo lors de sa relecture.
Le développement limité en 0 à l'ordre 3 de ;)(1+2x)

La formule ;)(1+x) = 1+x/2-x²/8+x³/16

lors de la correction le résultat est

=1+ 2/2x - 2x²/8 +2x²/16 + 2x³/16

=1 + x - x²/2 + x³/2

sachant que c'est aussi ce résultat dans un exo du cours

comment arriver à un dénominateur 2 pour toutes les fractions? je comprends pas
et puis même ya une fraction **/16 en trop !!!

[fatal_error]

salut,

parce que tas mal recopié.
;)(1+y) = 1+y/2-y²/8+y³/16
tu rempalces y par 2x...
1+x-(2x)^2/8+(2x)^3/16 = 1+x-4x^2/8 + 8x^3/16

[Sa Majesté]

Salut
Il faut remplacer x par 2x ... et (2x)^3 = 8x^3 ...

[ZBAR]

quoi?

j'ai dja remplacé plein de fois x par 2x

merci comme même mais je comprends toujours pas ...

[Sa Majesté]

[ZBAR]

lorsque je simplifie par 2 :



je trouve 1+x-(x^2)/4+x^3/8 :mur: comment t'as fait pour trouver deux dénominateur sur 2??

(merci beaucoup)

[XENSECP]

Bah si tu sais pas développer je pense qu'on peut rien pour toi


Idem pour


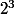
Erreurs d'inattention quand tu nous tiens !

[ZBAR]

Erreurs d'inattention quand tu nous tiens !

Beh en fait c'est que j'avais vraiment oublié que ça se faisait.. :marteau:
et bien merci beaucoup, ça va me sauver la mise!

(oh fait, j'ai une question, qu'est ce qui vous pousse à aider les gens qui ont des problèmes de mathématiques sur ce forum?) =)