Bonsoir, je bloque sur cet exo.
A et B jouent à pile ou face.
Pile ou face
2 messages
- Page 1 sur 1
par mehdi-128 » 25 Oct 2011, 05:10
Finalement j'ai réussi les 2 premières questions, mais je bloque sur la 3ème :
si l'on note a le nombre de piles sorties au cours des x parties on peut écrire ,b le nombre de faces sories on peut écrire
a+b=x
a-b=y
si j'ai bien compris le texte
donc y=2a-x avec a[0,n] donc les valeurs prises par y[-x;x]
il faut remarquer que y et x sont de même parité:
si x est pair x=2m=>y=2(a-m) donc y prend les valeurs -2m,-2(m-1),......0,2.....2(m-1),2m
si x est impair x=2m+1=>y=...
soit 
le nombre de sorties de pile au cours des x parties doit donc être égal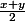
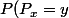=P(a=\frac{x+y}{2}))
mais a est entier
*si y n'a pas la même parité que x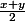n'est pas entier donc
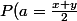=0=>P(P_x=y)=0)
*si x et y sont de même parité
soit
ce qui donne y appartient à [-x , x]
dans ce cas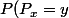=P(a=\frac{x+y}{2})=(_{\frac{x+y}{2}}^x) \frac{1}{2^{n}})
Pour la question 2, j'ai fait :
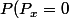=(_{n}^{2n})\frac{1}{2^{2n}}=\frac{1*3*...*(2n-1)}{2*4*...*2n})
si l'on note a le nombre de piles sorties au cours des x parties on peut écrire ,b le nombre de faces sories on peut écrire
a+b=x
a-b=y
si j'ai bien compris le texte
donc y=2a-x avec a[0,n] donc les valeurs prises par y[-x;x]
il faut remarquer que y et x sont de même parité:
si x est pair x=2m=>y=2(a-m) donc y prend les valeurs -2m,-2(m-1),......0,2.....2(m-1),2m
si x est impair x=2m+1=>y=...
*si y n'a pas la même parité que x
*si x et y sont de même parité
soit
dans ce cas
Pour la question 2, j'ai fait :
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :