Petite recurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 20:40
par leon1789 » 28 Aoû 2008, 20:40
juve1897 a écrit:comme

est le plus petit entier tel que
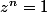
, il vient que

est un diviseur de

heu oui c'est ça, mais comment tu sais ça ?
Après on revient à l'exo de départ ... :id:
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 20:41
par juve1897 » 28 Aoû 2008, 20:41
leon1789 a écrit:heu oui c'est ça, mais comment tu sais ça ?
Après on revient à l'exo de départ ... :id:
ben je te l'avias deja dit dans l'autre exo et tu m'as dit non.
c'est pour ça que je ne comprenais plus rien lol.
Ben en fait c'est assez intuitif ce truc d'ordre non ??

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 20:44
par leon1789 » 28 Aoû 2008, 20:44
juve1897 a écrit:ben je te l'avias deja dit dans l'autre exo et tu m'as dit non.
oui, mais je ne pensais pas que tu avais compris :marteau:
juve1897 a écrit:Ben en fait c'est assez intuitif ce truc d'ordre non ??
ben on va voir ça sur l'exo principal :happy2:
Bon, tu fais un résumé de ce qu'on sait sur l'ordre (multiplicatif) de 5 modulo

:
modulo 
, on sait que

, donc l'ordre (multiplicatif) de 5 divise
truc.
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 21:08
par juve1897 » 28 Aoû 2008, 21:08
leon1789 a écrit:oui, mais je ne pensais pas que tu avais compris :marteau:
ben on va voir ça sur l'exo principal :happy2:
Bon, tu fais un résumé de ce qu'on sait sur l'ordre (multiplicatif) de 5 modulo

:
modulo 
, on sait que

, donc l'ordre (multiplicatif) de 5 divise
truc.
on a vu que

donc


-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 21:15
par leon1789 » 28 Aoû 2008, 21:15
Quand on a
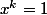
, c'est l'ordre de x qui divise k.
Ici ça donne :
juve1897 a écrit:on a vu que

donc

c'est plutôt

donc
w (l' ordre de 5) divise 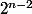
Que peut-on dire sur les diviseurs de
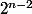
?
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 21:20
par juve1897 » 28 Aoû 2008, 21:20
leon1789 a écrit:Quand on a
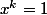
, c'est l'ordre de x qui divise k.
Ici ça donne :
c'est plutôt

donc
w (l' ordre de 5) divise 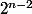
Que peut-on dire sur les diviseurs de
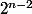
?
Mais c'est ce que j'ai dit en écrivant

Mais depuis hier tu me dis que non, je comprends pas pourquoi.
Je peux voir que tous les diviseurs de
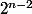
sont multiple de
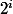
avec


-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 21:28
par leon1789 » 28 Aoû 2008, 21:28
juve1897 a écrit:Mais c'est ce que j'ai dit en écrivant

teuteuteuteu , tu as écrit

(dans Z), ce qui revient indirectement à l'égalité

parce qu'on est dans Z ! (ce serait faux dans d'autre circonstances comme

...)
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 21:30
par juve1897 » 28 Aoû 2008, 21:30
leon1789 a écrit:teuteuteuteu , tu as écrit

(dans Z), ce qui revient indirectement à l'égalité

parce qu'on est dans Z ! (ce serait faux dans d'autre circonstances comme

...)
je comprends pas, j'arrive pas à voir la nuance.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 21:34
par leon1789 » 28 Aoû 2008, 21:34
juve1897 a écrit:Je peux voir que tous les diviseurs de
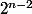
sont multiple de
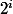
avec

non pas "multiple", mais
--> les diviseurs de
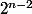
sont les entiers
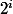
avec

OK !!!
Bon, donc l'ordre de 5 s'écrit
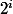
avec

On va montrer que i = n-2 ! (...sans raisonnement par l'absurde, trop moche...)
On part de

et

Dans Z, peux-tu factoriser

en
(......))
? c'est comme
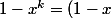(....))

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 21:42
par leon1789 » 28 Aoû 2008, 21:42
non pas "multiple", mais
--> les diviseurs de
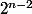
sont les entiers
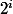
avec

OK !!!
Bon, donc l'ordre de 5 s'écrit
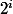
avec une certaine valeur de

On va montrer que i = n-2 ! (...sans raisonnement par l'absurde, trop moche...)
On part de

et

Dans Z, peux-tu factoriser

en
(......))
? c'est comme
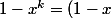(....))
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 21:45
par juve1897 » 28 Aoû 2008, 21:45
Ben je pense que
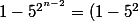 (1+\sum_{i=1}^{n-2} 5^{2^{i}} ))

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 21:49
par leon1789 » 28 Aoû 2008, 21:49
juve1897 a écrit:Ben je pense que
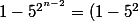 (1+\sum_{i=1}^{n-2} 5^{2^{i}} ))
heu, il faut 1- 5^{2^{n-2}} = (1 - 5^{
2^i}) (.........)
Par ailleurs, le i est fixé maintenant, on ne peut plus l'utiliser pour variable de sommation...
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 21:54
par juve1897 » 28 Aoû 2008, 21:54
leon1789 a écrit:heu, il faut 1- 5^{2^{n-2}} = (1 - 5^{2^i}) (.........)
Par ailleurs, le i est fixé maintenant, on ne peut plus l'utiliser pour variable de sommation...
Ce que j'ai ecrit plus haut est faux ???
JE comprends pas pq tu met
)
au lieu de
)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 21:56
par leon1789 » 28 Aoû 2008, 21:56
on a

et

Et je te propose de regarder le rapport entre

et
(....))
dans Z.
EDIT : Je te conseille de poser

pour soulager les écritures...
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 22:05
par juve1897 » 28 Aoû 2008, 22:05
leon1789 a écrit:on a

et

Et je te propose de regarder le rapport entre

et
(....))
dans Z.
EDIT : Je te conseille de poser

pour soulager les écritures...
Cet exo me rend dingue.
je comprends pas pourquoi tu persistes à mettre
)
à la place de
)
Explique moi stp
(je sais que je suis gonflante mais bon, c'est ça ou je ne comprends rien)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 22:08
par leon1789 » 28 Aoû 2008, 22:08
juve1897 a écrit:Cet exo me rend dingue.
je comprends pas pourquoi tu persistes à mettre
)
à la place de
)
Parce que l'ordre (multiplicatif) de 5 modulo

, c'est
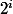
, pas 2 que je sache ! On sait que
 = 0 \ mod \ 2^n)
mais on ne sait rien sur
 \ mod \ 2^n)
...
Alors pourquoi veux-tu uniquement considérer
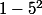
?? :marteau:
PS : je vais me coucher , A+
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 22:09
par juve1897 » 28 Aoû 2008, 22:09
leon1789 a écrit:Parce que l'ordre (multiplicatif) de 5 modulo 2^n , c'est
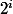
, pas 2 que je sache ! On sait que
 = 0 \ mod \ 2^n)
mais on ne sait rien sur
 \ mod \ 2^n)
...
Alors pourquoi veux-tu uniquement considérer 1-5^2 ?? :marteau:
PS : je vais me coucher , A+
bonne nuit.
Merci pour ton aide.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 29 Aoû 2008, 00:32
par skilveg » 29 Aoû 2008, 00:32
Bon, je prends le relais, mais je ne vais peut-être pas tarder non plus...
Je me permets de reprendre:
- on veut l'ordre de 5 modulo

;
- tu as montré que, si

est un entier supérieur à 2,

où

est un entier impair.
OK? Maintenant, regarde modulo

la suite des
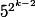
. Valent-ils 1 au bout d'un moment? Si oui, quand? Et qu'est-ce que ça nous apporte sur l'ordre de 5 modulo

?
J'ajouterais aussi que léon n'a pas tort et qu'une nuit de sommeil t'aiderait peut-être mieux que toutes nos explications à y voir plus clair! :we:
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 29 Aoû 2008, 00:39
par juve1897 » 29 Aoû 2008, 00:39
skilveg a écrit:Bon, je prends le relais, mais je ne vais peut-être pas tarder non plus...
Je me permets de reprendre:
- on veut l'ordre de 5 modulo

;
- tu as montré que, si

est un entier supérieur à 2,

où

est un entier impair.
OK? Maintenant, regarde modulo

la suite des
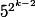
. Valent-ils 1 au bout d'un moment? Si oui, quand? Et qu'est-ce que ça nous apporte sur l'ordre de 5 modulo

?
J'ajouterais aussi que léon n'a pas tort et qu'une nuit de sommeil t'aiderait peut-être mieux que toutes nos explications à y voir plus clair! :we:
Malgré vos explications, je n'ai toujours pas compris, je ne sais mm pas ce qu'il faut chercher.
Ca fait 2 jours que je planche dessus et y'a rien qui en sort.
Je pense que je vais allée me coucher peut etre comme vous l'avez tous dit, ça ira mieux après.
Ben je vous remercie de votre aide une fois de plus.
Passez une bonne nuit.
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 29 Aoû 2008, 00:56
par skilveg » 29 Aoû 2008, 00:56
Bon, je vais me coucher aussi... Mais essaie de préciser l'endroit que tu ne comprends pas, et de mettre les choses à plat. Bonne nuit
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
est le plus petit entier tel que
, il vient que
est un diviseur de
, c'est l'ordre de x qui divise k.
donc w (l' ordre de 5) divise
?
sont multiple de
avec
et
et
dans Z.
pour soulager les écritures...
à la place de
;
est un entier supérieur à 2,
où
est un entier impair.
la suite des
. Valent-ils 1 au bout d'un moment? Si oui, quand? Et qu'est-ce que ça nous apporte sur l'ordre de 5 modulo
?