Petite recurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 22:33
par juve1897 » 27 Aoû 2008, 22:33
leon1789 a écrit:(...)un nombre impair 2p+1 car
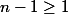
, ok .
Bon, la première récurrence est faite.
Maintenant, tu peux en déduire que l'ordre de 5 modulo 2^n est inférieure ou égale à "
truc"...
La dernière étape est de prouver que l'ordre ne peut pas être plus petit que "
truc" .
Mais c'est bien là mon probleme c'est que je ne vois pas le lien entre l'indication et le vrai probleme/
Peux tu m'énoncer le problème en d'autre termes s'il te plaît, car pour être honnête je ne comprends pas vraiment ce qu'il faut faire.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 22:36
par leon1789 » 27 Aoû 2008, 22:36
Tu as démontré ceci
par rec. sur n, que pour tout entier
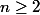
, on a
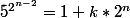
Vois-tu une puissance de 5 valant 1 modulo

?
Tu vois la définition de l'ordre que je t'ai donnée ?
Que peux-tu conclure pour l'instant ?
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 22:39
par juve1897 » 27 Aoû 2008, 22:39
leon1789 a écrit:Tu as démontré ceci
Vois-tu une puissance de 5 valant 1 modulo

?
Tu vois la définition de l'ordre que je t'ai donnée ?
Que peux-tu conclure pour l'instant ?
ben oui tout simplement n = 2
on a

mais je ne vois pas trop le rapport c'est ça qui me rend folle.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 22:44
par leon1789 » 27 Aoû 2008, 22:44
juve1897 a écrit:ben oui tout simplement n = 2
on a

mais nAAAAaaan ! Tu n'as pas le droit de fixer la valeur de

comme tu le veux. La valeur de

est figée par l'énoncé. Toi, tu dois donner un entier

tel que
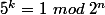
. :id:
Puis avec la définition de l'ordre, conclure une première inégalité.
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 22:51
par juve1897 » 27 Aoû 2008, 22:51
leon1789 a écrit:mais nAAAAaaan ! Tu n'as pas le droit de fixer la valeur de

comme tu le veux. La valeur de

est figée par l'énoncé. Toi, tu dois donner un entier

tel que
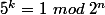
. :id:
Puis avec la définition de l'ordre, conclure une première inégalité.
Je sais que la reponse que tu attends est k = 2^{n-2} mais ...
Au risque de paraître bête, pourrais je te demander à nouveau ce que l'on cherche au juste là ???
On a montré que
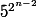
=

(avec k impair)
Mais je ne vois pas du tout en quoi cela nous amène à démonter que 5 a pour ordre
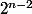
dans
)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 22:53
par leon1789 » 27 Aoû 2008, 22:53
Il faut montrer l'égalité
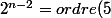)
où par définition
 = min \{ k \in N^* \ | \ 5^k = 1 \ mod 2^n \})
Pour l'instant, on a seulement une inégalité. Laquelle ?
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 23:11
par juve1897 » 27 Aoû 2008, 23:11
mais moi je ne comprends pas pourquoi

car si on utilise le th de fermat on c'est que si
 = 1)
alors

donc dans notre cas c'est

car pgcd(5,2) =1

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 23:16
par leon1789 » 27 Aoû 2008, 23:16
juve1897 a écrit:mais moi je ne comprends pas pourquoi

Ecoute, je crois que tu es fatiguée. Cette congruence, tu l'as démontré juste au-dessus (par récurrence) !
Repose toi, et demain, tu verras d'un coup d'oeil pourquoi

, et tu pourras terminer.
Bonne nuit. :dodo:
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 23:20
par juve1897 » 27 Aoû 2008, 23:20
leon1789 a écrit:Ecoute, je crois que tu es fatiguée. Cette congruence, tu l'as démontré juste au-dessus (par récurrence) !
Repose toi, et demain, tu verras d'un coup d'oeil pourquoi

, et tu pourras terminer.
Bonne nuit. :dodo:
j'ai tres bien vu que


mais c'est bizarre franchement car le th de Fermat dit autre chose.
Alors s'il te plait, pourras tu m'aider encore un peu car là je vais m'arracher les cheveux (car ça à l'air tout con)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 23:25
par leon1789 » 27 Aoû 2008, 23:25
juve1897 a écrit:mais c'est bizarre franchement car le th de Fermat dit autre chose.
Alors s'il te plait, pourras tu m'aider encore un peu car là je vais m'arracher les cheveux (car ça à l'air tout con)
Mais le théorème de Fermat n'a rien à voir la dedans :
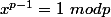
si pgcd(x,p)=1 et
p premier.
Est-ce que

est premier ?
Et puis, ce n'est pas parce que
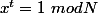
qu'on ne peut pas avoir
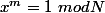
avec

!
Donc il n'y a vraiment pas lieu de croire que le théo de Fermat contredit le résultat.
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 23:29
par juve1897 » 27 Aoû 2008, 23:29
leon1789 a écrit:Mais le théorème de Fermat n'a rien à voir la dedans :
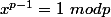
si pgcd(x,p)=1 et
p premier.
Est-ce que

est premier ?
Et puis, ce n'est pas parce que
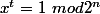
qu'on ne peut pas avoir
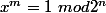
avec

!
Donc il n'y a vraiment pas lieu de croire que le théo de Fermat contredit le résultat.
Oui c'est vrai, de plus il n'y a rien qui me dit que

est premier
Mais franchement le résultat est il si trivial que ça ???

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 23:32
par leon1789 » 27 Aoû 2008, 23:32
juve1897 a écrit:Oui c'est vrai, de plus il n'y a rien qui me dit que

est premier
Heu... rien ne te dit que

est premier ?!?!
Lorsque

, on sait que

n'est pas premier ! :marteau:
juve1897 a écrit:Mais franchement le résultat est il si trivial que ça ???
mais non, ton exo n'est pas simple. Il demande un peu de travail. Tu en a fait une moitié.
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 23:38
par juve1897 » 27 Aoû 2008, 23:38
Mais le plus marrant de l'histoire, c'est que cet exo fait parti d'annales d'examen.
Et cette question n'en est qu'une petite parmi tant d'autre (un sujet à faire en 2 heures) et moi j'ai mis presque 3heures si ce n'est plus à faire la moitié.
De plus il y'a une question supplémentaire qui découle du résultat que je dois trouver.
Je suis pas sorti de l'auberge.
Peux tu m'aider s'il te plait (si ce n'est pas trop te demander)

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 23:41
par leon1789 » 27 Aoû 2008, 23:41
juve1897 a écrit:Peux tu m'aider s'il te plait (si ce n'est pas trop te demander)
Pour toi (comme pour moi), je pense que le mieux sera demain :id:
:dodo:
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 23:44
par juve1897 » 27 Aoû 2008, 23:44
comme tu voudras.
Merci pour l'aide que tu m'as apporté.
En tous cas moi je vais continuer à réfléchir sur le sujet. :marteau:
J'espère pouvoir résoudre cette récurrence.
Merci.
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 23:59
par juve1897 » 27 Aoû 2008, 23:59
Désolée d'être si insistante mais y'aurait il une personne pour m'aider à continuer mon exo ???
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 14:41
par juve1897 » 28 Aoû 2008, 14:41
je pense que

avec k ordre de 5 dans

mais ensuite je ne vois pas trop comment continuer.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 16:03
par leon1789 » 28 Aoû 2008, 16:03
Avant de continuer, que sais-tu sur l'ordre (noté

par exemple) d'un élément

et l'ensemble des entiers

tels que
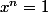
?
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 16:15
par juve1897 » 28 Aoû 2008, 16:15
leon1789 a écrit:Avant de continuer, que sais-tu sur l'ordre (noté

par exemple) d'un élément

et l'ensemble des entiers

tels que
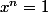
?
il faut que ce w (qui est l'ordre) soit le plus petit entier tel que


-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 16:21
par leon1789 » 28 Aoû 2008, 16:21
il faut que ce w (qui est l'ordre) soit le plus petit entier
naturel tel que
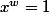
oui, plus petit au sens de la comparaison

et, ce qui revient au même en réalité, aussi au sens de la divisibilité.
Est-ce que tu comprends ce que cela signifie "être le plus petit au sens de la divisibilité" ?
Cela signifie que
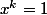
implique "w divise k".
C'est ok pour toi ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
, ok .
