Petite recurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 20:40
par juve1897 » 27 Aoû 2008, 20:40
Bonsoir,
j'essaie de résoudre un problème:
Montrez par récurrence sur n, que pour tout entier 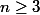 , 5 a pour ordre
, 5 a pour ordre 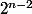 dans
dans *)
Je ne vois pas comment faire, pourriez vous me guider ?
Merci
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 27 Aoû 2008, 20:43
par Doraki » 27 Aoû 2008, 20:43
C'est pas plutot (Z / 2^n.Z)* ?
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 20:47
par juve1897 » 27 Aoû 2008, 20:47
oui c'est ça, j'arrivais pas à l'ecrire .
Tu es dans ma classe où quoi lol ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 20:52
par leon1789 » 27 Aoû 2008, 20:52

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 20:55
par leon1789 » 27 Aoû 2008, 20:55
écris 5 =1+2^2 ... c'est la ruse cet exo je crois
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 20:55
par juve1897 » 27 Aoû 2008, 20:55
leon1789 a écrit:Ah ça me rappelle ma jeunesse ! Je me souvent de ce résultat assez surprenant... Bon, j'essaie de retrouver une démo...
Ben le prof a mis une indication si ça peut t'aider :
Indication: Montrez par rec. sur n, que pour tout entier
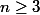
, on a
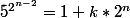
où k est un nombre entier impair.
Meme avec l'indication je vois pas comment faire.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 27 Aoû 2008, 20:55
par Doraki » 27 Aoû 2008, 20:55
Tiens pourquoi ils ont pas mis n>=2 plutot =/
T'arrives pas la récurrence ou t'arrives pas à te ramener à l'indication ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 20:58
par leon1789 » 27 Aoû 2008, 20:58
Doraki a écrit:Tiens pourquoi ils ont pas mis n>=2 plutot =/
Effectivement... :id:
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 20:59
par juve1897 » 27 Aoû 2008, 20:59
En fait j'ai du mal avec l'expression "a pour ordre".
J'ai pas compris ce que ça voulait dire.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 21:01
par leon1789 » 27 Aoû 2008, 21:01
Démontre ça pour commencer
juve1897 a écrit: Montrez par rec. sur n, que pour tout entier
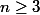
, on a
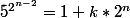
où k est un nombre entier impair.
Tu fais une récurrence (hé hé c'est écrit) en commençant par
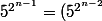^2 = ...)
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 21:17
par juve1897 » 27 Aoû 2008, 21:17
Doraki a écrit:Tiens pourquoi ils ont pas mis n>=2 plutot =/
T'arrives pas la récurrence ou t'arrives pas à te ramener à l'indication ?
Ben l'indication je ne comprends pas trop le 1 + k * 2^n =
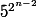
Et pour la récurrence je réfléchis encore.
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 21:26
par juve1897 » 27 Aoû 2008, 21:26
JE suis desolée d'insister mais j'ai pas compris ce que voulais dire "5 a pour ordre
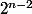
Car pour moi dire que 5 a pour ordre 2 dans
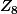
(pour n = 3) ça veut rien dire.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 21:44
par leon1789 » 27 Aoû 2008, 21:44
juve1897 a écrit:Car pour moi dire que 5 a pour ordre 2 dans
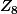
(pour n = 3) ça veut rien dire.
Cela signifie que la plus petite puissance de 5 congrue à 1 modulo 8 est 5^2 :zen:
De manière générale, si x appartient à un groupe G multiplicatif,
 = min \{ n \in N^* \ | \ x^n =1_G \})
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 21:52
par juve1897 » 27 Aoû 2008, 21:52
Merci pour ta def de l'ordre/
En effectuant la recurrence je reste bloquée la.
n = 3
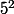
= 1 + 3*
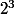
Supposons vrai jusqu'à l'ordre n
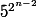
= 1 + k *

Montrons qu'elle st vraie pour n+1
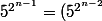^2)
=
^2)
= 1 +
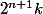
+
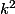
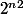
j'ai continue a développer mais ça ne me mene à rien
Peux tu m'aider à continuer STP.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 22:08
par leon1789 » 27 Aoû 2008, 22:08
Montre que
^2)
est multiple de
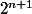
. Quel est le quotient ? Et la parité du quotient ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 22:11
par leon1789 » 27 Aoû 2008, 22:11
juve1897 a écrit:Merci pour ta def de l'ordre/
En effectuant la recurrence je reste bloquée la.
n = 3
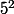
= 1 + 3*
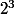
Tu as vu que cela fonctionne aussi pour n=2 ? :we:
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 22:15
par juve1897 » 27 Aoû 2008, 22:15
leon1789 a écrit:Montre
^2)
est multiple de
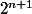
. Quel est le quotient ? Et la parité du quotient ?
jai continué en faisant ceci:
^2)
=
)
=
)
Mais apres je vois plus trop quoi faire.
EDIT : En fait je viens de me rendre compte que
)
=
}_{K})
Nous avons donc bien la forme attendu

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 22:19
par leon1789 » 27 Aoû 2008, 22:19
juve1897 a écrit:Mais apres je vois plus trop quoi faire.
Tu es fatigué : tu as oublié ce que tu voulais démontrer dans cette récurrence.
Que peux-tu dire de
)
... avec

.
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 27 Aoû 2008, 22:25
par juve1897 » 27 Aoû 2008, 22:25
leon1789 a écrit:Tu es fatigué : tu as oublié ce que tu voulais démontrer dans cette récurrence.
Que peux-tu dire de
)
... avec

.
J'ai fait un edit en haut.
On a la forme
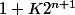
avec
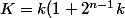)
nous pouvons dire que K est impair
car k est impair et
)
est l'écriture d'un nombre impair (2p + 1)
est ce que je me trompe

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 22:30
par leon1789 » 27 Aoû 2008, 22:30
(...)un nombre impair 2p+1 car
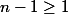
, ok .
Bon, la première récurrence est faite.
Maintenant, tu peux en déduire que l'ordre de 5 modulo 2^n est inférieure ou égale à "
truc"...
La dernière étape est de prouver que l'ordre ne peut pas être plus petit que "
truc" .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités