Petite recurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 16:28
par juve1897 » 28 Aoû 2008, 16:28
leon1789 a écrit:oui, plus petit au sens de la comparaison

et, ce qui revient au même en réalité, aussi au sens de la divisibilité.
Est-ce que tu comprends ce que cela signifie "être le plus petit au sens de la divisibilité" ?
Cela signifie que
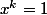
implique "w divise k".
C'est ok pour toi ?
oui j'ai compris que tout les n tel que

sont des multiples de w qui est le plus petit des n.
donc

avec

est ce que c'est ça ???
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 28 Aoû 2008, 16:39
par Doraki » 28 Aoû 2008, 16:39
Non, tu ce que tu compares, c'est des ordres comme n et w, jamais les éléments du groupe, ça veut rien dire de comparer des éléments du groupe.
5 est d'ordre w dans (Z/ mZ)* ça veut dire que w est le plus petit des ordres n>0 tels que 5^n = 1 (mod m).
Ca veut donc dire que 5^w = 1 (mod m), et que pour tout n avec 0Tu n'as jamais à comparer un 5^n avec un 5^n', ça ne voudrait rien dire de pertinent par rapport au problème posé.
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 17:09
par juve1897 » 28 Aoû 2008, 17:09
Franchement je commence vraiment à en avoir marre de cet exo.
Je comprends pas trop, est ce que vous pourriez m'expliquer clairement ce qu'il faut rechercher et faire, car là on tourne en rond depuis hiersoir.
Je cherche à comprendre comment marche l'ordre, le résultat je m'en fou un peu. Donc si une explication claire pouvait m'etre donnée elle serait la bienvenue.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 17:31
par leon1789 » 28 Aoû 2008, 17:31
C'est clair que pour faire cet exo, il faut déjà avoir reçu un cours minimum sur l'ordre d'un élément. Prends un livre où tout ça est expliqué. Ou peut-être qu'une âme très charitable te fera un petit cours sur le forum (?)...
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 17:55
par juve1897 » 28 Aoû 2008, 17:55
Serais-tu cette âme charitable?
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 18:14
par juve1897 » 28 Aoû 2008, 18:14
Super ton lien !
Lol y'a rien écrit, c'est un article laissé à rédaction.
En tous cas si tu pouvais au moi m'aider à terminer cet exo ça serait gentil.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 18:16
par leon1789 » 28 Aoû 2008, 18:16
juve1897 a écrit:Super ton lien !
J'ai eu des problèmes de copier/coller, mais maintenant, c'est bon, le lien fonctionne.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 18:17
par leon1789 » 28 Aoû 2008, 18:17
juve1897 a écrit:En tous cas si tu pouvais au moi m'aider à terminer cet exo ça serait gentil.
Tu as constaté que la première moitié de l'exo était laborieuse.
Pour le terminer dans de bonnes conditions, il faut quand même comprendre de quoi il est question dans l'énoncé :de l'ordre d'un élément...
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 18:26
par juve1897 » 28 Aoû 2008, 18:26
leon1789 a écrit:Tu as constaté que la première moitié de l'exo était laborieuse.
Pour le terminer dans de bonnes conditions, il faut quand même comprendre de quoi il est question dans l'énoncé :de l'ordre d'un élément...
Ben j'attendrais que quelqu'un m'apporte son aide à ce niveau là

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 18:32
par leon1789 » 28 Aoû 2008, 18:32
juve1897 a écrit:Ben j'attendrais que quelqu'un m'apporte son aide à ce niveau là
En fait, il faut au moins faire un exercice préliminaire pour essayer de comprendre ce qu'est l'ordre d'un élément. Une définition ne suffit pas pour comprendre.
Bon, je te propose de faire un autre exo avant de terminer celui en cours.
Ok ?
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 18:41
par juve1897 » 28 Aoû 2008, 18:41
leon1789 a écrit:En fait, il faut au moins faire un exercice préliminaire pour essayer de comprendre ce qu'est l'ordre d'un élément. Une définition ne suffit pas pour comprendre.
Bon, je te propose de faire un autre exo avant de terminer celui en cours.
Ok ?
Oui merci s'il te plait.
Car cette histoire d'ordre m'a rendu folle.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 19:21
par leon1789 » 28 Aoû 2008, 19:21
juve1897 a écrit:Oui merci s'il te plait.
Car cette histoire d'ordre m'a rendu folle.
Ben c'est pas fini, car on va faire un exo sur l'ordre de certains éléments.
Bon, on va changer le cadre : on passe dans l'ensemble des nombres complexes C.
Question simple pour commencer : quels sont les entiers relatifs n tels que

.
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 19:28
par juve1897 » 28 Aoû 2008, 19:28
leon1789 a écrit:Ben c'est pas fini, car on va faire un exo sur l'ordre de certains éléments.
Bon, on va changer le cadre : on passe dans l'ensemble des nombres complexes C.
Question simple pour commencer : quels sont les entiers relatifs n tels que

.
ben je pense que c'est
^n)
avec n impair

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 19:32
par leon1789 » 28 Aoû 2008, 19:32
juve1897 a écrit:ben je pense que c'est
^n)
avec n impair
heu oui, mais c'est pas mieux que ma question :ptdr:
Il faut répondre : ce sont les nombres n = ....
EDIT : je viens de lire ta réponse ! ben, c'est pas ça du tout !!!!
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 19:38
par juve1897 » 28 Aoû 2008, 19:38
leon1789 a écrit:heu oui, mais c'est pas mieux que ma question :ptdr:
Il faut répondre : ce sont les nombres n = ....
ok ben je dirais que ce sont les nombres

avec
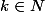

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 19:45
par leon1789 » 28 Aoû 2008, 19:45
juve1897 a écrit:ok ben je dirais que ce sont les nombres

avec
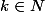
naaaaan,

!
Quels sont les

tels que

??? :hum:
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 19:54
par juve1897 » 28 Aoû 2008, 19:54
leon1789 a écrit:naaaaan,

!
Quels sont les

tels que

??? :hum:
Ecoute je suis vraiment fatiguée, alors excuse les betises que j'ecris.
Donc après réflexion, je pense que c'est

avec


-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 28 Aoû 2008, 20:08
par leon1789 » 28 Aoû 2008, 20:08
juve1897 a écrit:Ecoute je suis vraiment fatiguée, alors excuse les betises que j'ecris.
on peut reprendre plus tard...
juve1897 a écrit:Donc après réflexion, je pense que c'est

avec

oui ok
Ici, tu viens de dire que ce sont les entiers
multiples de 4.
Et bien 4, c'est l'ordre (multiplicatif) de i dans
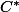
.
Seconde question :
on considère un nombre complexe z et un entier n tels que
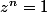
.
Soit w le plus petit entier naturel non nul tel que

.
Montrer que w divise n.
Indication : division euclidienne de n par w...
-
juve1897
- Membre Relatif
- Messages: 355
- Enregistré le: 22 Aoû 2007, 15:11
-
 par juve1897 » 28 Aoû 2008, 20:19
par juve1897 » 28 Aoû 2008, 20:19
leon1789 a écrit:on peut reprendre plus tard...
oui ok
Ici, tu viens de dire que ce sont les entiers
multiples de 4.
Et bien 4, c'est l'ordre (multiplicatif) de i dans
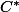
.
Seconde question :
on considère un nombre complexe z et un entier n tels que
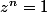
.
Soit w le plus petit entier naturel non nul tel que

.
Montrer que w divise n.
Indication : division euclidienne de n par w...
comme

est le plus petit entier tel que
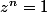
, il vient que

un diviseur de n donc

c'est fini on a

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
et, ce qui revient au même en réalité, aussi au sens de la divisibilité.
implique "w divise k".
