Petit exo sur les sev...

[pouik]

Bonjour,
Pourries-vous m'aider à traiter cet exercice sur lequel je ne sais pas bien ou je vais. Merci d'avance.

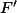
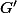
Soit un espace vectoriel, soient et deux sous-espaces vectoriels de . Soit un supplémentaire de inter dans , soit un supplémentaire de inter dans . Démontrer la relation :
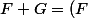
inter

[fahr451]

bonjour

as tu démontré de façon immédiate l'égalité des sommes?

restera la question de la somme directe pour la seconde.

[pouik]

bah en fait je vois pas trop comment le rediger, mais je vois bien que F' + F inter G décrit F tout entier et que G' + F inter G décrit G tout entier, donc on peut dire qu'on a bien F + G tout entier mais pour la rédaction, ca coince vraiment. :briques: :briques:

[fahr451]

F = (Finter G)+F '

G = (Finter G )+G' donc

F+G = (Finter G)+(Finter G) + F' +G ' = (Finter G) +F ' +G'


car A+A = A pour A sev

[pouik]

ok c'est compris,
mais pour ce qui est de la somme directe, comment puis-je m'y prendre ? car je ne vois pas bien comment procéder !

[fahr451]

comment montre t on que la somme de trois sev est directe?

[pouik]

comment montre t on que la somme de trois sev est directe?

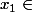
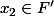
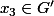
Il suffit de montrer que si on prend (F inter G), et , alors :


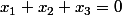
mais je ne vois pas bien comment faire...

[fahr451]

hum je ne crois pas ...

si on suppose de plus que
x1+x2+x3 = 0
alors x1= x2=x3=0

[pouik]

hum je ne crois pas ...

si on suppose de plus que
x1+x2+x3 = 0
alors x1= x2=x3=0

Désolé mais je n'ai pas bien compris votre remarque... :triste: :triste:

[fahr451]

hum je ne crois pas ...

si on suppose de plus que
x1+x2+x3 = 0
alors x1= x2=x3=0

c'est ça la définition


crois tu que si on prend trois vecteurs quelconques la somme est nulle ?

tu confonds conclusion et hypothèse

on suppose que la somme est nulle on montre que les trois vecteurs sont nuls

[pouik]

d'accord, mais comment peut on fair pour montrer que les 3 vecteurs sont alors nuls.
Quand on a deux sev, là ca va mais avec trois j'avoue etre un peu perplexe. :doh:

[fahr451]

-x1-x2= x3

donc x3 est dans F donc dans F inter G étant dans G' il est nul

[pouik]

-x1-x2= x3

donc x3 est dans F donc dans F inter G étant dans G' il est nul

désolé mais je ne comprend pas l'implication : etre dans F implique etre dans (F inter G),
pour moi c'est plutot l'inverse. Non ?? :hein:

[fahr451]

x1 est dans F inter G donc F
x2 dans F

donc x3 dans F
or x3 dans G' donc G donc dans Finter G

[pouik]

d'accord donc on a

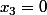
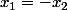
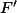
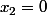
et ensuite , or est dans (F inter G) donc est dans (F inter G), or est dans donc puis

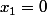
est-ce correct ??

[fahr451]

oui ça l 'est

[pouik]

merci beaucoup pour votre aide.