Permutation avec répétition
25 messages
- Page 1 sur 2 - 1, 2
Permutation avec répétition
Hello,
je . bloque sur une question de proba et dénombrement
20 personnes dans une queue pour acheter un billet de spectacle à 5euros
13 personnes on un billet de 5€
7 on un billet de 10€
la caisse commence avec zero euro de monnaie
quelle est la proba que le caissier ait tojours assez de monaie?
Il semble que ça soit des histoires de permutation avec répétition
Donc, on arrive à connaitre le nombre d’arrangement possible N= 20!/(13!x7!) = 77 520
Mais à partir de là comment on exclut les arrangements qui ne répondent pas à la conditions, puisqu’il faut que il y ait toujours plus de personnes avec 5 euro que de personne avec des 10 euros dans l’ordre d’apparition…?
merci de votre aide
je . bloque sur une question de proba et dénombrement
20 personnes dans une queue pour acheter un billet de spectacle à 5euros
13 personnes on un billet de 5€
7 on un billet de 10€
la caisse commence avec zero euro de monnaie
quelle est la proba que le caissier ait tojours assez de monaie?
Il semble que ça soit des histoires de permutation avec répétition
Donc, on arrive à connaitre le nombre d’arrangement possible N= 20!/(13!x7!) = 77 520
Mais à partir de là comment on exclut les arrangements qui ne répondent pas à la conditions, puisqu’il faut que il y ait toujours plus de personnes avec 5 euro que de personne avec des 10 euros dans l’ordre d’apparition…?
merci de votre aide
Re: Permutation avec répétition
on peut remarquer la similitude avec :
je pars de 0 (billets de 5€)
je compte +1 (pour 5€)
je compte -1 (pour 10€)
on cherche une chaîne type chaîne de Markov ou 'problème du saut de puce' telle que :
_ les valeurs soient toujours positives
_ l'arrivée soit à (13-7) = 6
je pars de 0 (billets de 5€)
je compte +1 (pour 5€)
je compte -1 (pour 10€)
on cherche une chaîne type chaîne de Markov ou 'problème du saut de puce' telle que :
_ les valeurs soient toujours positives
_ l'arrivée soit à (13-7) = 6
Re: Permutation avec répétition
Hi,
Inspiré de pascal du dessus et du connu:
On note (i,j) l'etat ou i est le nb de 1 et j le nb de 0, resp les mecs a 5 et 10. (Par ex letat (3,2) contient 11010)
Si a chaque etape on ajoute un 1 ou un 0 als les predecesseurs sont (i-1,j) (ss reserve que i-1>=j) ou (i, j-1)
On peut creer un tableau auquel on va rajouter des lignes petit a petit
La k ieme ligne note les etat (k,c) ou c est la colonne.
L elem indexé (k,c) est un entier représentant le nombre de paths valides, partant depuis 1 et contenant k 1 et c 0.
Le remplissage de (k,c) consiste a ajouter le nombre a gauche et le nombre au dessus (resp (k,c-1) et (k-1,c))
Evidemmet on sarrete de remplir la ligne lorsque c==k ou c==7(symboliquement, au complete la ligne par des 0)
On recup le nombre en (13,7)
Il y a certainement une relation avec pascal pour pas se farcir toutes les sommes (env 2*(7*8/2+6*7))
Depuis mobile, jai pas de papier/outils pour checker
Inspiré de pascal du dessus et du connu:
On note (i,j) l'etat ou i est le nb de 1 et j le nb de 0, resp les mecs a 5 et 10. (Par ex letat (3,2) contient 11010)
Si a chaque etape on ajoute un 1 ou un 0 als les predecesseurs sont (i-1,j) (ss reserve que i-1>=j) ou (i, j-1)
On peut creer un tableau auquel on va rajouter des lignes petit a petit
La k ieme ligne note les etat (k,c) ou c est la colonne.
L elem indexé (k,c) est un entier représentant le nombre de paths valides, partant depuis 1 et contenant k 1 et c 0.
Le remplissage de (k,c) consiste a ajouter le nombre a gauche et le nombre au dessus (resp (k,c-1) et (k-1,c))
Evidemmet on sarrete de remplir la ligne lorsque c==k ou c==7(symboliquement, au complete la ligne par des 0)
On recup le nombre en (13,7)
Il y a certainement une relation avec pascal pour pas se farcir toutes les sommes (env 2*(7*8/2+6*7))
Depuis mobile, jai pas de papier/outils pour checker
la vie est une fête 
Re: Permutation avec répétition
Bonjour
Avant tout, de mon point de vue, c'est plutôt un exercice de dénombrement que de proba.
Soit N le nombre des arrivées pour lesquelles il n'y aura pas assez de monnaie à un certain moment (donc N-77520 est le nombre d'arrivées pour lesquelles il y a aura assez de monnaie) alors
la probabilité demandée est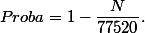
Donc la solution consiste à déterminer N.
Le dénombrement donne N=38760. (remarque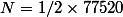 )
)
On a alors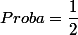
Avant tout, de mon point de vue, c'est plutôt un exercice de dénombrement que de proba.
Soit N le nombre des arrivées pour lesquelles il n'y aura pas assez de monnaie à un certain moment (donc N-77520 est le nombre d'arrivées pour lesquelles il y a aura assez de monnaie) alors
la probabilité demandée est
Donc la solution consiste à déterminer N.
Le dénombrement donne N=38760. (remarque
On a alors
Re: Permutation avec répétition
Salut
Je viens de voir que fatal_error a fait à peu près pareil.
Je mets quand même:
on a une grille 7*13
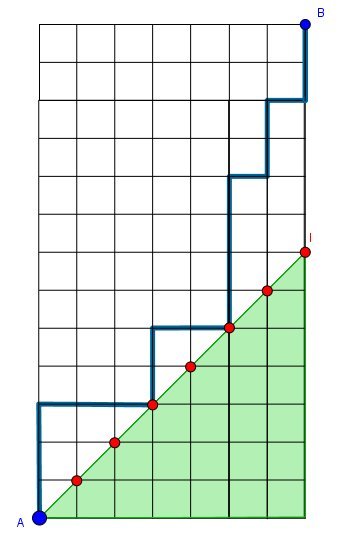
Il faut compter le nombre de chemins pour aller de A à B en allant soit vers la droite, soit vers le haut, sans aller dans la zone verte, mais les points rouges sont admis.
Avec le trajet bleu, les clients paient successivement:
5-5-5-10-10-10-5-5-10-10-5-5-5-5-10-5-5-10-5-5
De proche en proche, en commençant par les points proches de B (on peut s'aider d'un tableur) j'arrive à 38760 donc la proba demandée 38760/77520=1/2
Ce serait bien de généraliser.
Je viens de voir que fatal_error a fait à peu près pareil.
Je mets quand même:
on a une grille 7*13
Il faut compter le nombre de chemins pour aller de A à B en allant soit vers la droite, soit vers le haut, sans aller dans la zone verte, mais les points rouges sont admis.
Avec le trajet bleu, les clients paient successivement:
5-5-5-10-10-10-5-5-10-10-5-5-5-5-10-5-5-10-5-5
De proche en proche, en commençant par les points proches de B (on peut s'aider d'un tableur) j'arrive à 38760 donc la proba demandée 38760/77520=1/2
Ce serait bien de généraliser.

Re: Permutation avec répétition
Si le nombre de billets de 5 était égal au nombre de billets de 10, on aurait un nombre de Catalan.
Re: Permutation avec répétition
par programmation :
38760 cas favorables
38760 cas défavorables
soit p=1/2
Aviateur, comment tu fais ton dénombrement ?
38760 cas favorables
38760 cas défavorables
soit p=1/2
Aviateur, comment tu fais ton dénombrement ?
Re: Permutation avec répétition
bon, pas malin..(comme d'hab  )
)
depuis nombre de catalan cf chan) https://en.wikipedia.org/wiki/Catalan_number
je tombe sur lattice path https://en.wikipedia.org/wiki/Lattice_path dont la formule semble etre (k,n)
comme toujours de la biere dans le sang je peux pas me debrouiller..
je tape 38760 oeis dans google
https://oeis.org/A000579
c'est pas loin...
mais en tapant half triangle pascal,
je tombe sur
http://oeis.org/A008315
où "May 23 2004
T(n,k) is the number of n-digit binary words (length n sequences on {0,1}) containing k 1's such that no initial segment of the sequence has more 1's than 0's. - "
qui correspond quasiment à notre cas (on a interchangé 1 et 0)
1999:
T(n, k) = binomial(n, k) - binomial(n, k-1). - Michael Somos, Aug 17 1999
verification:
T(20,7) = (20,7) - (20,6) = 38760
qui a l'air correcte.
(j'ai testé avec n==10, k==3 et l'algo (en lequel j'ai plus confiance (tristement))
me retourne bien 75
edit:
apparemment, formule démontrée ici https://cs.uwaterloo.ca/journals/JIS/VO ... walks.html (4)
mais là j'ai les yeux éclatés donc stop pour moi ..
 )
)depuis nombre de catalan cf chan) https://en.wikipedia.org/wiki/Catalan_number
je tombe sur lattice path https://en.wikipedia.org/wiki/Lattice_path dont la formule semble etre (k,n)
comme toujours de la biere dans le sang je peux pas me debrouiller..
je tape 38760 oeis dans google
https://oeis.org/A000579
c'est pas loin...
mais en tapant half triangle pascal,
je tombe sur
http://oeis.org/A008315
où "May 23 2004
T(n,k) is the number of n-digit binary words (length n sequences on {0,1}) containing k 1's such that no initial segment of the sequence has more 1's than 0's. - "
qui correspond quasiment à notre cas (on a interchangé 1 et 0)
1999:
T(n, k) = binomial(n, k) - binomial(n, k-1). - Michael Somos, Aug 17 1999
verification:
T(20,7) = (20,7) - (20,6) = 38760
qui a l'air correcte.
(j'ai testé avec n==10, k==3 et l'algo (en lequel j'ai plus confiance (tristement))
- Code: Tout sélectionner
var oks = [];
const N = 10;
const nbZeros = 3;
var denum = 0;
for(var i = 0; i<Math.pow(2,N);++i){
var bin = i.toString(2).padStart(N, '0');
var arr = bin.split('');
if(valid(arr)){
oks.push(arr);
}
if(arr.filter(x=>x==0).length==nbZeros){denum++}
}
rep = dispatch(oks);
console.log(oks)
console.log(rep);
console.log('p = ', `${oks.length} '/' ${denum} == ${oks.length/denum}`);
function dispatch(arr){
dic = {};
arr.forEach(v=>{
x = v.join('').replace(/0+$/, '');
var l = v.length - x.length;
dic[l] = dic[l] || 0;
dic[l]++;
})
return dic;
}
function valid(arr){
var a = 0;
var b = 0;
for(var i = 0; i < arr.length; ++i){
if(arr[i] == 1){
a++;
}else{
b++;
}
if(a < b){
return false;
}
}
if(b != nbZeros){
return false;
}
return true;
}
me retourne bien 75
edit:
apparemment, formule démontrée ici https://cs.uwaterloo.ca/journals/JIS/VO ... walks.html (4)
mais là j'ai les yeux éclatés donc stop pour moi ..
la vie est une fête 
Re: Permutation avec répétition
Bonjour,
@pascal16
Pour dénombrer combien il y a de cas où il n'y aura pas assez de monnaies, il faut les partitionner en les différentes situations possibles et chacun se dénombre facilement de la même façon.
Ce qui fait alors au total=38760 .)
Maintenant il y a une autre façon de faire encore plus immédiate. On met en bijection chaque cas où il y aura assez de monnaie avec chaque cas où il n'y a pas assez de monnaie. C'est pas compliqué mais assez difficile à expliquer, non pas que ne sache pas le faire (i.e expliquer sans baragouiner mais c'est un peu long.) De plus accompagné d' un dessin cela serait serait plus parlant mais ...(c'est aussi long à faire)
Ce qui fait/2=38760.)
@pascal16
Pour dénombrer combien il y a de cas où il n'y aura pas assez de monnaies, il faut les partitionner en les différentes situations possibles et chacun se dénombre facilement de la même façon.
Ce qui fait alors au total
Maintenant il y a une autre façon de faire encore plus immédiate. On met en bijection chaque cas où il y aura assez de monnaie avec chaque cas où il n'y a pas assez de monnaie. C'est pas compliqué mais assez difficile à expliquer, non pas que ne sache pas le faire (i.e expliquer sans baragouiner mais c'est un peu long.) De plus accompagné d' un dessin cela serait serait plus parlant mais ...(c'est aussi long à faire)
Ce qui fait
Re: Permutation avec répétition
Pour 10 clients (3 avec 10€ et 7 avec 5€) on arrive à une proba de 75/120
D'accord ?
D'accord ?
Re: Permutation avec répétition
slt chan,
oui
3,10: p = 75 '/' 120 == 0.625
un autre au cas où pour la (mal)"chance":
4,12:
p = 275 '/' 495 == 0.5555555555555556
application de 4,12:
C(4,12) - C(3,12) = 275
evidemment le denom c'est juste C(4,12) (et resp C(3,10) pour 3,10)
oui
3,10: p = 75 '/' 120 == 0.625
un autre au cas où pour la (mal)"chance":
4,12:
p = 275 '/' 495 == 0.5555555555555556
application de 4,12:
C(4,12) - C(3,12) = 275
evidemment le denom c'est juste C(4,12) (et resp C(3,10) pour 3,10)
la vie est une fête 
Re: Permutation avec répétition
merci pour ces différentes façons de faire.
perso, je pensais faire des traitements en binaires, pas très compliqué en C/C+/C++, mais j'ai pas fait de C depuis un moment.
Je suis parti du C#
-> une liste de binaires qui représente un nombre n base 2, mais aussi nos 2 cas possibles
-> une fonction qui remplace "++" sur cette liste pour balayer la liste comme un nombre
-> une fonction qui vérifie la "signature" : ici 6 en caisse à la fin
-> une fonction qui vérifie la "négativité" : ici si on ne peut pas rendre la monnaie
et la boucle principale devient alors faisable niveau collège.
perso, je pensais faire des traitements en binaires, pas très compliqué en C/C+/C++, mais j'ai pas fait de C depuis un moment.
Je suis parti du C#
-> une liste de binaires qui représente un nombre n base 2, mais aussi nos 2 cas possibles
-> une fonction qui remplace "++" sur cette liste pour balayer la liste comme un nombre
-> une fonction qui vérifie la "signature" : ici 6 en caisse à la fin
-> une fonction qui vérifie la "négativité" : ici si on ne peut pas rendre la monnaie
et la boucle principale devient alors faisable niveau collège.
Re: Permutation avec répétition
Salut
Une autre façon de dénombrer les "bons" trajets (toujours assez de monnaie).
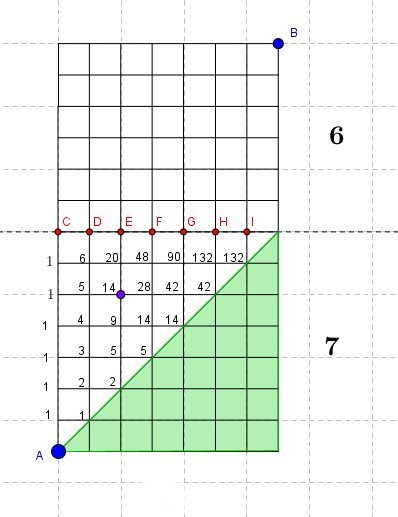
On commence par calculer, en commençant près de A, le nombre de façons d'arriver aux différents points du triangle symétrique du vert. Il y a par exemple 14 façons d'aller de A au point violet sans aller à l'intérieur de la zone verte.
On partitionne ensuite les trajets en fonction du premier point rouge atteint sur la droite en pointillés.
On a donc en tout, pour aller de A à B:
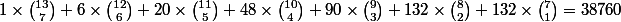
Une autre façon de dénombrer les "bons" trajets (toujours assez de monnaie).

On commence par calculer, en commençant près de A, le nombre de façons d'arriver aux différents points du triangle symétrique du vert. Il y a par exemple 14 façons d'aller de A au point violet sans aller à l'intérieur de la zone verte.
On partitionne ensuite les trajets en fonction du premier point rouge atteint sur la droite en pointillés.
On a donc en tout, pour aller de A à B:
Re: Permutation avec répétition
@chan si tu pouvais avec ton logiciel faire le dessin suivant:
Tu prends un exemple de trajectoire qui correspond à une situation où il n'y a pas assez de monnaie.
Si possible une trajectoire qui passe 2 fois dans la zone en vert pour que cela soit assez parlant.
Alors tu dessines sa trajectoire "duale", i.e la trajectoire obtenue à partir la précédente en remplaçant la partie qui passe dans la partie en vert par son symétrique par rapport à la droit y=x.
Cela permettra de voir la bijection dont j'ai parlé dans mon message précédent et de voir aussi sans calcul que P=1/2.
Tu prends un exemple de trajectoire qui correspond à une situation où il n'y a pas assez de monnaie.
Si possible une trajectoire qui passe 2 fois dans la zone en vert pour que cela soit assez parlant.
Alors tu dessines sa trajectoire "duale", i.e la trajectoire obtenue à partir la précédente en remplaçant la partie qui passe dans la partie en vert par son symétrique par rapport à la droit y=x.
Cela permettra de voir la bijection dont j'ai parlé dans mon message précédent et de voir aussi sans calcul que P=1/2.
Re: Permutation avec répétition
Merci @chan. D'abord bien vu et puis tes dessins sont forts utiles pour la bijection que je veux montrer.
Alors je me rend compte que je me suis planté dans mes explications, c'est pas ça ma bijection.
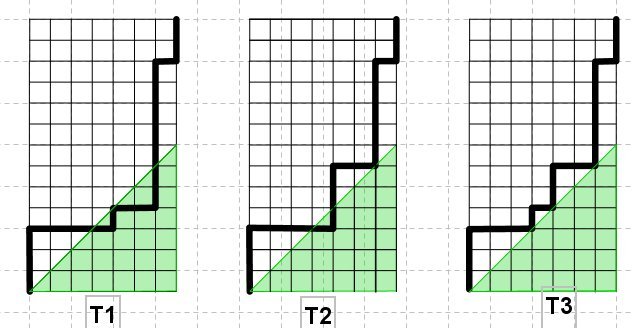
Pour T_1 je lui associe la trajectoire suivante:
La première fois que je rentre dans le carré vert donc
" je fais un pas à droite puis un pas vers le haut" alors je change la trajectoire par "un pas vers le haut puis un pas à droite. "
Donc là pas de pb ça donne le début de "T_3."
La deuxième fois que je rentre dans le carré vert je fais
" 2 pas vers la droite suivit de 7 pas vers le haut" que j'échange par " 7 pas vers le haut puis 2 pas vers la droite" (c'est là que je me suis mal expliqué.)
ça veut dire que ce n'est plus T_3 mais une autre trajectoire.
Bien sûr la même procédure associe à T_2 la trajectoire T_3.
Sauf erreur j'ai une bijection entre les deux classes de trajectoires.
Alors je me rend compte que je me suis planté dans mes explications, c'est pas ça ma bijection.
Pour T_1 je lui associe la trajectoire suivante:
La première fois que je rentre dans le carré vert donc
" je fais un pas à droite puis un pas vers le haut" alors je change la trajectoire par "un pas vers le haut puis un pas à droite. "
Donc là pas de pb ça donne le début de "T_3."
La deuxième fois que je rentre dans le carré vert je fais
" 2 pas vers la droite suivit de 7 pas vers le haut" que j'échange par " 7 pas vers le haut puis 2 pas vers la droite" (c'est là que je me suis mal expliqué.)
ça veut dire que ce n'est plus T_3 mais une autre trajectoire.
Bien sûr la même procédure associe à T_2 la trajectoire T_3.
Sauf erreur j'ai une bijection entre les deux classes de trajectoires.
Re: Permutation avec répétition
Il y a bien des bijections entre ces deux ensembles puisqu'ils ont le même nombre d'éléments. Elles ne me paraissent pas simples à préciser. On tombe sur 1/2 avec les nombres 7 et 13.
Avec 1 client de plus( avec 5 €), le nombre de trajets est:
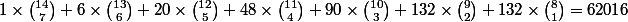
donc proba égale à 62016/116280
Avec 1 client de plus( avec 5 €), le nombre de trajets est:
donc proba égale à 62016/116280
Re: Permutation avec répétition
proposition de formule
n clients dont p ont des billets de 10€ et les autres de 5€
proba pour que la monnaie puisse être rendue
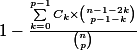
avec
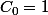
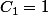
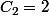
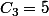
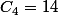
...
nombres de Catalan
n clients dont p ont des billets de 10€ et les autres de 5€
proba pour que la monnaie puisse être rendue
avec
...
nombres de Catalan
Re: Permutation avec répétition
Bonjour
Je pensais avoir démontré que le nombre de cas où on n'a pas la monnaie valait
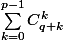
où p est le nombre de billets à 10E et q à 5E (on a donc n=p+q).
En tout cas c'est bien ce que j'ai retrouvé pour p=7 et q=13 puis 14.
Je pensais avoir démontré que le nombre de cas où on n'a pas la monnaie valait
où p est le nombre de billets à 10E et q à 5E (on a donc n=p+q).
En tout cas c'est bien ce que j'ai retrouvé pour p=7 et q=13 puis 14.
Re: Permutation avec répétition
salut
On dirait que ça revient au même ...
pour (n,p)=(10,3) les deux formules donnent 45
pour (n,p)=(11,3) les deux formules donnent 55
On dirait que ça revient au même ...
pour (n,p)=(10,3) les deux formules donnent 45
pour (n,p)=(11,3) les deux formules donnent 55
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 94 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :